trójkąt
Pytanie: Przepraszam wie ktoś jak sprawdzić czy trójkąt o bokach √3 , √6 i p {8} jest rozwartokatny?
10 maj 20:15
@Basia:
Zastosować tw.cosinusów. Jeżeli cosinus dla któregoś kąta będzie ujemny ⇒
kąt∊(90;180) ⇒ tr. jest rozwartokątny
10 maj 20:20
Jacek Karaśkiewicz:
Można np. z tw. Carnota (cosinusów).
Oznaczmy kąt naprzeciwko boku o długości
√8 przez α.
Mamy: (
√8)
2 = (
√3)
2 + (
√6)
2 − 2
√3√6cosα
8 = 9 − 6
√2cosα
6
√2cosα = 1
Ponieważ cosα > 0, więc α < 90
o.
Kąt α był największym kątem w tym trójkącie, gdyż leżał naprzeciwko najdłuższego boku, więc
trójkąt ten nie jest rozwartokątny.
10 maj 20:21
Jacek Karaśkiewicz:
Spóźniony, sorry : − )
10 maj 20:22
Bogdan:
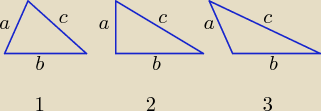
Proponuję następującą analizę:
a ≤ b ≤ c
1. Trójkąt ostrokątny: a
2 + b
2 > c
2
2. Trójkąt prostokątny: a
2 + b
2 = c
2
3. Trójkąt rozwartokątny: a
2 + b
2 < c
2
W tym zadaniu: a =
√3, b =
√6, c =
√8
a
2 = 3, b
2 = 6, c
2 = 8
3 + 6 > 8, a więc trójkąt jest ostrokątny.
10 maj 20:32