Znajdź funkcję odwrotną do f(x): krystek: Znajdź funkcję odwrotną do f(x): f(x)=y= x²; D_f=(−∞,0)

krystek: bo ogólnie nie pamiętam jak wyznaczyć x z równania y=x² , jeżeli z definicji wynika że x<0 , zatem nie mogę spierwiastkować

krystek: *znaczy z dziedziny wynika że x<0

ZKS: x² jest zawsze nieujemne więc możemy spierwiastkować tylko że zakładamy że y ≥ 0. y = x² / √ zał. y ≥ 0 |x| = √y x = ±√y

krystek: dziękuję, a jak mam znowu y=x²; tylko D_f=<1:+∞) to będzie tak samo?

ZKS: Według mnie tak.

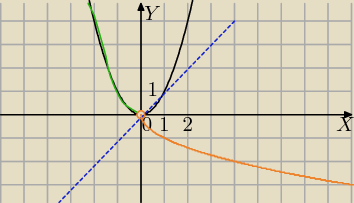
Mila: y=x² i D_f=(−∞,0) x=−√y [ponieważ lewa strona ujemna z założenia, to przed pierwiastkiem jest (−)] zamieniamy zmienne: y=−√x

krystek: mam jeszcze jeden podpunkt z tego zadania z którym mam problem:

	2x
f(x)=		Df= (−∞;−1]
	1+x2

	2x
y=		/*(1+x2)
	1+x2

y+yx²=2x yx²−2x+y=0 Δ=4−4y²=4(1−y²)

	2−2√1−y2		1−√1−y2
x1=		=
	2y		y

	2+2√1−y2		1+√1−y2
x2=		=
	2y		y

i nie wiem jak dalej

krystek: Ktoś zabrał mój nick ?

krystek222: oddaję czy mógłby mi ktoś jeszcze pomóc z tym ostatnim przykładem

ZKS:

	1 ± √1 − y2
x =
	y

Nie zapomnij o dziedzinie.

krystek222: dziękuję, ale czy jednego nie trzeba odrzucić

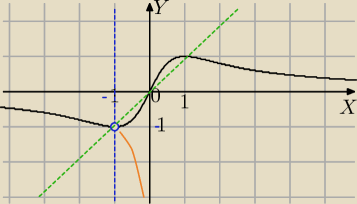
Mila: Trzeba odrzucić x₁. zbadaj zbiór wartości f(x) dla x<−1 Wykresy mają być symetryczne do siebie względem prostej y=x

	1+√1−x2
y=		(wykres pomarańczowy ,trochę niedokładny) )
	x

1−√1−x2
	<−1 brak rozwiązań.
x

krystek222: dziękuję