najmniejsza wartość lauren: na bokach prostokąta o obwodzie 12 opisano półkola. jakie wymiary powinien mieć prostokąt tak aby pole figury było najmniejsze?

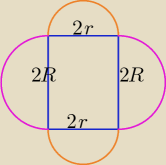
Eta: a= 2r, b= 2R Ob= 4r+4R = 12 ⇒ r+R= 3 ⇒ R= 3−r, dla r€ (0,3) P(figury)= a*b+πr²+πR² = 4rR+πr²+πR² P(r) = 4r(3−r)+πr²+π(3−r)²=........ = (2π−4)r²+(12−6π)r+9π −−− to f. kwadratowa parabola ramionami do góry, zatem osiąga mnimum dla odciętej wierzchołka paraboli

	−(12−6π
rmin=		= ... = 1,5
	2*(2π−4)

to R_min = 3−r= 1,5 zatem takim prostokątem spełniającym warunki zadania jest kwadrat o boku długości 3

Siusiak: XxxxxxDDDDDD