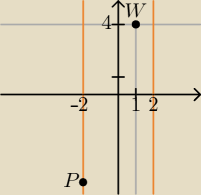
wykres funkcji alo: Wykresem funkcji kwadratowej jest parabola, której wierzchołkiem jest punkt W(1,4). Najmniejsza wartość funkcji f w przedziale <−2,2> wynosi −5 Przedstaw wzór funkcji f w postaci kanonicznej. wzór nie musi byc w postaci kanoniczej moge sama przekształcic ale jakby ktos dał jakiś pomysł na to zadanie byłabym wdzięczna

Bogdan: Postać kanoniczna f(x) = a(x − 1)² + 4 P= (−2, −5) ⇒ a * (−2 − 1)² + 4 = 5 stąd wyznaczamy a.

Bogdan: Poprawka: a * (−2 − 1)² + 4 = −5, stąd wyznaczamy a.

alo: a skąd wiemy że wykres przechodzi akurat przez punkt −2 przeciez może przechodzić przez każdy w tym przedziale?

Mickej:

alo: ajj sorki już wiem co i jak dzieki

Bogdan: Dla jakiej wartości x: x = −2 czy x = 2 podana funkcja osiąga wartość −5?

alo: może osiągnąć −5 dla obu chyba?

Bogdan: Wróćmy więc do rozwiązania zadania. a * (−2 − 1)² + 4 = −5 ⇒ a = −1 f(x) = −(x − 1)² + 4 f(−2) = −9 + 4 = −5 f(2) = −1 + 4 = 3 3 ≠ −5 Widać zresztą z rysunku, że f(−2) ≠ f(2)

alo: zrozumiałam! dziekuje

alo: szczerze mówiąc analizując to jeszcze to: −5 jest funkcja stałą więc i gdy podstawimy pod wzór x=2 a będzie wówczas wynosiło −9 a po sprawdzeniu równanie będzie poprawne będzie wynosiło −5 gdy x=−2 a wynosi −1 a po sprawdzeniu równanie równiez bedzie wynosiło −5 wiec nadal nie wiem o co chodzi ale trudno. dziekuje za zainteresowanie

alo: a nie źle sprawdziłam, jednak dobrze