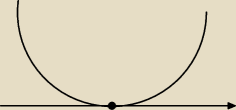
Rozwiąż nierówność. x+1/x>=2 maths: Rozwiąż nierówność. x+1/x≥2 Moje rozwiązanie: D: x≠0 (x²+1)/x − 2x/x≥0 /*x x²−2x+1≥0 (x−1)²≥0 więc odczytuje z powyższego rysunku kiedy to jest ≥ 0 i powinno być że dla x∊ℛ/{0}

maths: sprawdzam w takim jednym programie i okazuje się że jest to źle...

sushi_gg6397228: zapis nieczytelny

licznik
	−−> stosuj taki zapis na ulamek
mianownik

maths:

	1
x+		≥2
	x

Mam nadzieję że sobie teraz poradzisz z odczytaniem...

Basia:

	1
x+		≥ 2
	x

x2+1		2x
	−		≥ 0
x		x

x2−2x+1
	≥ 0
x

(x+1)2
	≥ 0
x

policz wartość dla x= −2 i zastanów się jeszcze raz nad tą odpowiedzią "zjadłeś" mianownik

maths:

	(x+1)2
A powiedz mi jeżeli wyznaczyłem dziedzinę D: x≠0 to nie moge w takiej sytuacji		≥0
	x

pomnożyć przez x aby się go pozbyć?

Basia: niestety nie, bo x≠0 wprawdzie, ale może być i dodatnie i ujemne czyli nie wiesz jak zachowa się nierówność (x+1)² ≥ 0 dla każdego x∊R no to aby ułamek był nieujemny 1. licznik dodatni i mianownik dodatni lub 2. licznik=0 i wtedy mianownik nieważny czyli x≠−1 i x>0 lub x=−1 co daje {−1}∪(0;+∞)

maths: aha ok, dzięki za pomoc

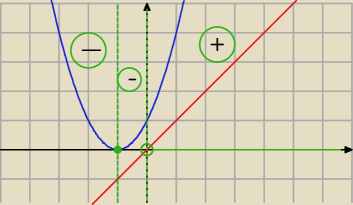
Basia: a to jest najprostszy sposób wykres licznika; wykres mianownika albo fala