Do jakich x należą? Dominik: Siemka do jakich x należą 2/x+3/(2−x)−5<=0 mi wychodzi funkcja kwadratowa, ale na tablicy ktoś zrobił z tego wielomian i przedział x−ów był rozszerzony o jeszcze inne wartości....

Mati_gg9225535: popraw zapis a moze ktos sie podejmie pomocy

Eta: taka ma być ta nierówność:

	2
		−5 ≤0
	x+3   2−x

Basia: Witaj Eto chyba to /x+3/ jest wartością bezwzględną

Dominik: Ma być taka 2/x + 3 / (2−x) − 5 <=0

sushi_gg6397228: chłopak robi wszystko, by Was zniechęcić

Eta: Witaj Basiu Czort wie, co tam ma być ? i mamy: "zgaduj−zgadulę"

Eta: 2|x+3|*(2−x)−5≤0 .... taka?

Mati_gg9225535:

2|x + 3|
	− 5≤0 tak ?
2−x

Mati_gg9225535: ale przynajmniej wiemy jaki znak

Eta: Jaki "zwrot"! ......... a nie znak

Mati_gg9225535: przepraszam ale zrozumiałaś więc się nie czepiaj haha

Eta: Dobra ... jaka treść,takie rozwiązanie! czyli ... brak rozwiązania

sushi_gg6397228: a moze to jest implikacja ?

Mati_gg9225535: rozwiazania nie udzielimy co najwyzej mozna chłopakowi pozostawić wskazówki

Mati_gg9225535: implikacja w odwrotną stronę miałoby sens.......

Dominik: bez wartości bezwzg. przecież to są kreski ułamkowe, jeszcze raz POWOLI (2/x) + 3/(2−x) −5 <=0 / jest to kreska ułamkowa, reszta wg, kolejności wykonywania działań... xD

Mati_gg9225535: o jakas trzecia forma równania

2		3
	+		− 5 ≤ 0
x		2−x

Mati_gg9225535: ach nierówności*

Eta:

2		3
	+		−5≤0
x		2−x

Mati_gg9225535: w takim razie, licz dziedzinę, sprowadz do wspolnego mianownika a potem wykorzystaj fakt, że

	a
		≤0 ⇔ ab≤0
	b

Basia: ta równoważność jest fałszywa

	5
5*0 = 0 ale		nie istnieje
	0

a
	≤0 ⇔ [ a*b≤0 ∧ b≠0 ]
b

Mati_gg9225535: no dobrze, ale b w tym przypadku ≠ 0 załatwia dziedzina ;>

Dominik: Mati_gg9225535: właśnie o taki przykład mi chodzi, no właśnie czy dziedzinę traktuję jako zbiór na osi x?

Mati_gg9225535: tak, dziedzina to te x dla których równanie / nierówność ma rozwiązania rzeczywiste

Eta: D=R\{0,2}

2(2−x)+3x−5*x(2−x)
	≤0
x(2−x)

uporządkuj licznik i otrzymasz:

	5x2−9x+4
		≤0 ⇔ x(2−x)(5x2−9x+4)≤0 ⇔ x(2−x)(x−1)(5x−4)≤0
	x(2−x)

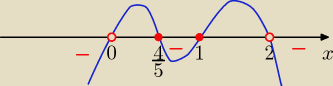
"fala " od dołu po prawej stronie i podaj odp: x€...........

Basia: dziedzina załatwia sprawę w zadaniu, ale nie załatwia tego, że napisałeś równoważność fałszywą

Mati_gg9225535: dobrze Basiu, bede pamietał na przyszłość i dzieki za uwagę

Dominik: Mianowicie jeśli rozwiążę tą nierówność otrzymuję pierwiastki x₁=⁴₅ x₂=1 Natomiast ktoś na tablicy rozwiązał to tak x należy do ( −∞,0) ∪ <⁴₅,1> ∪ <2,+∞)

Dominik: oks, dzięki za odp. teraz to rozumiem!

Eta: