Gustlik:
Wskazówka:
Dziedzina:
ad a) x+3>0 ⇒ ... (liczba logarytmowana musi być dodatnia)
ad b) x≥0 i sin
√x≥0 (pod pierwiastkiem musi być liczba nieujemna)
ad c) ma być
√5−2x, tak? Jeżeli tak, to 5−2x≥0 patrz pkt. b
ad d) 1−2cosx>0 − patrz pkt. a.
Zbiór wartości:
ad a) E=R, logarytm moze przyjąć każdą wartość (patrz rysunek, np. y=lnx)
ad b) E=<0, 1>
ad c) E=<0, +
∞)
ad d) Dla funkcji 1−2cosx:
cosx€<−1, 1> /*(−2)
−2cosx€<−2, 2> /+1
1−2cosx€<−1, 3>
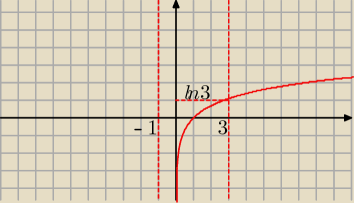
Badamy teraz, jak zachowa się logarytm naturalny dla argumentów należących do przedziału <−1,
3> − patrz rysunek:
E=(−
∞, ln3>
 Wskazówka:
Dziedzina:
ad a) x+3>0 ⇒ ... (liczba logarytmowana musi być dodatnia)
ad b) x≥0 i sin√x≥0 (pod pierwiastkiem musi być liczba nieujemna)
ad c) ma być √5−2x, tak? Jeżeli tak, to 5−2x≥0 patrz pkt. b
ad d) 1−2cosx>0 − patrz pkt. a.
Zbiór wartości:
ad a) E=R, logarytm moze przyjąć każdą wartość (patrz rysunek, np. y=lnx)
ad b) E=<0, 1>
ad c) E=<0, +∞)
ad d) Dla funkcji 1−2cosx:
cosx€<−1, 1> /*(−2)
−2cosx€<−2, 2> /+1
1−2cosx€<−1, 3>
Badamy teraz, jak zachowa się logarytm naturalny dla argumentów należących do przedziału <−1,
3> − patrz rysunek:
E=(−∞, ln3>
Wskazówka:
Dziedzina:
ad a) x+3>0 ⇒ ... (liczba logarytmowana musi być dodatnia)
ad b) x≥0 i sin√x≥0 (pod pierwiastkiem musi być liczba nieujemna)
ad c) ma być √5−2x, tak? Jeżeli tak, to 5−2x≥0 patrz pkt. b
ad d) 1−2cosx>0 − patrz pkt. a.
Zbiór wartości:
ad a) E=R, logarytm moze przyjąć każdą wartość (patrz rysunek, np. y=lnx)
ad b) E=<0, 1>
ad c) E=<0, +∞)
ad d) Dla funkcji 1−2cosx:
cosx€<−1, 1> /*(−2)
−2cosx€<−2, 2> /+1
1−2cosx€<−1, 3>
Badamy teraz, jak zachowa się logarytm naturalny dla argumentów należących do przedziału <−1,
3> − patrz rysunek:
E=(−∞, ln3>