Relacje Basiek: RELACJE Będę szczera− zadań mam z tego sporo, nie umiem nawet zacząć. Każda pomoc w tym zakresie będzie naprawdę bardzo mile widziana. Proponuję zacząć od czego [dla innych] banalnego. Sprawdzić, które własności spełnia relacja: a) S=A² A={0,2} [chodzi o zbadanie, czy jest *zwrotna, *symetryczna, *antysymetryczna, *przechodnia, *zupełna] Ew. ktoś może zarzucić mi tytułem literatury jakieś pomocnej też.

Basiek: Nic z tego nie będzie?

Saizou : Basiek po pierwsze witaj, dawno cię nie widziałem niestety nie pomogę bo moja znajomość matematyki ogranicza się do początków trygonometrii

sushi_gg6397228: zrob tabelke taka jak do statkow 2x2

Basiek: Cześć Saizou− witaj. Tłumaczę się: moja nieobecność jest spowodowana brakiem dostępu do globalnej sieci... Kolejny raz będę za min. tydzień. Straszna sprawa. I ech, tej znajomości trygonometrii w zasadzie też Ci zazdroszczę.

Saizou : " jak nie masz dostępu do sieci to nie istniejesz" . Swoją drogą to gdzie ty żyjesz?

Basiek: Sushi− wiem, o co Ci chodzi. Widziałam takie cudeńko na str. 44 jakiejś książki z 1986r. Mam. To udowadnia zwrotność, ale co z resztą?

Basiek: Saizou− jak na ironię: same centrum Krakowa. Zadania ściągam w weekendy jak przyjeżdżam do domu... i sypie mi się cały tydzień, a z matematyki nie wiem nic. W zasadzie z niczego nic nie wiem. Masakra.

Saizou : co cię nie zabije to cię wzmocni ale w sercu Krakowa nie ma internetu, to ja jestem w głębokim szoku

Basiek: Z moim szczęściem... wszystko jest możliwe. Tzn. internet jest. Wszyscy mają oprócz mojego mieszkania.

Basiek: Pomijając wszystko inne, może ktoś wie, jak sprawdzić przechodniość Przypomnę : ∀x,y∊R [(x,y)∊S ⋀ (y,x)∊S]⇒ (x,z)∊S} Dla przykładu S=A² A={0,2}

sushi_gg6397228: a jaki byl przepis ?

Basiek: No to właśnie nie wiem, nie ogarniam tego zupełnie. A próbowałam. W każdej książce jest o tym dosłownie jedna strona. I to w każdej to samo− niemalże sama teoria.

Saizou : może ja się nie znam ale to może pomoże http://www.math.edu.pl/relacje https://docs.google.com/viewer?a=v&q=cache:r7iXuZSMwT0J:sirjoker.w.interia.pl/mat/dyskr/Relacje.pdf+relacje+matematyka&hl=pl&gl=pl&pid=bl&srcid=ADGEESgDvUY_2_jke7J2hnhNoI7DnOPWonahD9wWguhEirNztvpOlzvO1pN1AiaYk4q4wa4ASc7tYukITLxe_UZaXDHYErVxIT8hAJPFsGz409hv5PXEyAG9YGAk2LISBf-ntoSVgX7j&sig=AHIEtbROrw-BbzX2fmQOCWMrcMzHxrsbQg

sushi_gg6397228: musi byc przepis typu x ρ y <==> x+y= 3 tam tylko podany jest zbior skad bierzemy "x" i "y" a nie ma przepisu

Basiek: Saizou− to pierwsze znam na pamięć. Zastosować nie umiem. A to drugie... to jest chyba na podstawie jakiejś tam bardziej zaawansowanej wiedzy matematycznej [niektóre sformułowania], a my niestety od tego zaczęliśmy. :<

Basiek: Sushi− przepisałam wszystko. "przepisy" są w przykładach od b−l

sushi_gg6397228: zrob zdjecie tego przykladu

Basiek: http://imgur.com/DSVLJ Podpunkt a.

sushi_gg6397228: to cos zgubili, bo zakreslenie calej tabelki=== wszystkie wlasnosci relacji

Basiek: A nie można gdzieś tam stwierdzić, że skoro mamy dwa różne elementy, to z=x lub z=y ?

sushi_gg6397228: zostaw "a" licz pozostale jak nie ma przepisu to skad wiesz ze ma byc x=y ?

Basiek: To jest matematyka− nie wiem. Zgaduję, zakładam, robię cokolwiek.

sushi_gg6397228: moze byc x+y= 2

Basiek: Nie widzi mi się to.., przecież− równie dobrze to może być para liczb {2,2} lub {0,0}... CHYBA.

PuRXUTM: czy matematyka na studiach jest aż tak straszna ?

Basiek: Z mojej perspektywy owszem. Ale to pewnie zależy. Ja spodziewałam się mniej... i prostszą. I najlepiej, żeby ktoś zaczął od małego powtórzonka. Ale co tam...

PuRXUTM: A Ty Basiek co studiujesz i gdzie jeśli można wiedzieć?

Basiek: UEK, finanse i rachunkowość. Jak na ironię zasypano mnie... matematyką. A gdzieś tam czekają na mnie inne dziwactwa.

PuRXUTM: ja myślę o matmie stosowanej na UJ ale nie wiem po tym co tu widzę i co słyszę o matmie na pierwszym roku to nie wiem co mam powiedzieć, może coś poradzicie ? studiuje ktoś tam ? albo ktoś ze znajomych ?

Basiek: Nie, nie znam nikogo, kto by się na matmę rzucił. Ale wiesz− jeśli to właśnie lubisz, czujesz, że to jest Twoje miejsce, to nie patrz na innych. Ja cierpię, bo zwyczajnie narobiłam sobie zaległości... teraz nagle wszystko. A relacji nie łapałam już na wykładzie. A potem to już całkowita klapa. Ale ja to ja.

PuRXUTM: a na ile zdałaś matmę na maturzę ?

Basiek: podstawa 100, rozsz. 76.

PuRXUTM: o kurde i ty masz problemy ? No czyli trzeba się wziąść ostro do pracy

Basiek: Hm, wykłady+ zadania są na platformie e−learningowej. Jestem odcięta od internetu, więc... z miejsca mam gigantyczne zaległości. Chciałam nadrobić chociaż część tych relacji, bo się teraz przewijają, ale chyba nie da rady jednak. Cudownie. Z tego, co widzę, to pracujesz cały czas... także spoko, będzie dobrze.

PuRXUTM: oby a ogólnie matma na studiach to jakiś kosmos czy jakoś idzie ogarnąć ( chodzi mi o sam początek np. pierwsze półrocze )?

Basiek: Właśnie zaczęłam. Po dwóch wykładach i dwóch ćwiczeniach: Wszystkie funkcje, cała logika, f. cyklometryczne, iloczyn kartezjański, relacje, ciągi, limesy, metryka. Mnie jest ciężko.

sushi_gg6397228: poflirtowalas sobie, chcesz robic te zadania czy nie?

Basiek: Nie flirtuję. Chyba, że z wolframem. Jak mam robić coś, czego nie umiem zacząć? No, naprawdę nie umiem.

sushi_gg6397228: napisalem, ze 'a" odpuszczamy zabieramy sie za 'b"

PuRXUTM: dzięki za informacje na pewno się przydadzą. A Ty nie przejmuj się tylko rób swoje. Dasz radę

sushi_gg6397228: x r y <==> |X|= |Y|

Basiek: Nie ma za co. Okej. Więc... b... S⊂R², (x,y)∊S ⇔|x|=|y| *zwrotna: ∀x∊R (x,x)∊S ⇔ ∀x∊R |x|=|x| (dobrze?) co jest spełnione dla x∊R=> relacja jest zwrotna.

sushi_gg6397228: a) zwrotnosc x r x musi byc prawda |X|= |x| −−> widac ze jest b) symetrycznosc jak zamienimy x z y na miesjca, czy dostaniemy to samo prawda

Basiek: *symetryczność |x|=|y|⇒|y|=|x| zawsze spełnione. Że tak?

Mila: Podaję Linka. Tam są dobre materiały. Których relacji nie zrobiłaś? http://pbc.biaman.pl/Content/610/ZiM-Kacprzak-Kacprzak.pdf

Basiek: *antysymetryczność" |x|=|y| ⇔ |y|=x lub |y|=−x ⇔ y=x lub y=−x ≠ y=x Nie spełnione (?)

Mila: Sushi też mnie to (a) zdeprymowało. Jeśli masz świeżą wiedzę, to czy przypadkiem nie jest to kwadrat kartezjański? Robię (d)

Basiek: Mila− niczego z tego i jeszcze... innych też nie. Robiłam iloczyn kartezjański, funkcje cyklometryczne... A to coś próbowałam, ale nie rozumiem, więc − przeznaczyłam ten czas na coś innego z zakresu matematyki. Dziękuję za link, na pewno zostanie wykorzystany. Niestety w książkach, czy to starszych, czy młodszych− niewiele jest o relacjach.

sushi_gg6397228: musi sama troche porobic, a nie na gotowce liczyc

sushi_gg6397228: poza tym trzeba wiedziec, ze jezeli jest taka i taka, to nie moze byc siaka i owaka to ułatwi prace zawsze mozna chociaz troche sprobowac zrobic tabelke i z rysunku popatrzec, jaka moze byc (jak nie spelnia warunku, to podac kontrprzyklad)

Basiek: Ależ ja chętnie zrobię. Tylko chciałabym się dowiedzieć, od czego zacząć. Zresztą, gotowce gotowcami, ale raczej nikt mi tych 30−tu przykładów nie zrobi.

sushi_gg6397228: http://www.math.edu.pl/rodzaje-relacji

sushi_gg6397228: moze najlepiej zaczac od prostych przykladow A= {1,2,3} relacja: a) x+y= 4 b) x=y c) x=2y

Basiek: Patrz: 21:37. Mam teorię. Jestem zasypana książkami. Przedpotowe, nowe,... Teoria mi niewiele daje, skoro nie umiem jej zastosować. A nie umiem.

sushi_gg6397228: czyli robimy a) tabelka i zaznaczamy "x" w polu dla ktorego nalezy dana para

Basiek: Co prawda tabelki widziałam, ale tylko w takich starszych książkach, ale jasne. Chętnie się czegoś nauczę. Czyli a) y=4−x One są określone dla A², tak? Zaznaczam {1,3}{2,2}{3,1} dla b) {1,1} {2,2} {3,3} dla c) {1,2} −> tylko

Mila: d)relacja : (x,y)∊S⇔|x−y|≤1 1) zwrotność:(x,x)∊S⇔|x−x|≤1 |x−x|=0<1 relacja zwrotna 2) symetryczność (x,y)∊S⇔(y,x)∊S |x−y|≤1⇔|y−x|≤1 relacja symetryczna 3) przechodnia? (x,y)∊S i (y,z)∊S⇔(x,z)∊S ? |x−y|≤1i |y−z|≤1 tu podaję kontrprzyklad x=1,y=2, z=3 |1−2|=1, |2−3|=1 , |1−3|=2>1 relacja nie jest przechodnia. Oczywiście zapisałam bez kwantyfikatorów, zobacz jak , bylo na wykładzie.

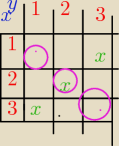
sushi_gg6397228: przekatna co zawiera kólka nazywamy Δ zwrotnosc to musza byc w kólkach rózowych " zielone x" czyli Δ⊂ relacji symetria r=r⁻¹ czyli jak zamienimy "x" z "y" to musimy dostac to samo przechodnia r o r ⊂ r ( jak złozymy dwa punkty, to musi powstac trzeci co tez jest w tabelce) przeciwsymetryczna r ∩ r⁻¹ =∅ = c przeciwzwrotna Δ ∩ r = ∅ antysymetryczna r ∩ r⁻¹ ⊂Δ spojna r ∪ r⁻¹ = cala tabelka

AC: Co do zadania a Relacja S składa się następujących par S={(0;0); (0;2); (2;0); (2;2)} zwrotność jest bo: elementy (0;0) i (2;2) należą do relacji symetryczność jest bo: (0;0)∊S ⇒ (0;0)∊S (0;2)∊S ⇒ (2;0)∊S (2;0)∊S ⇒ (0;2)∊S (2;2)∊S ⇒ (2;2)∊S przechodność też jest ∀(x;y)∊S ∧ (y;z)∊S ⇒ (x;z)∊S bo każda para z A² należy do S

sushi_gg6397228: patrzac na tabelke widzimy zwrotnosc brak symetria ok przeciwzrotnosc brak reszte trzeba pokombinowac

Mila: Nie mogę się połączyć ze stroną z Twoimi relacjami. napisz b i c bo sSushi nie robi.

Mila: AC .

Basiek: Przepraszam, przepisywałam Twoją odpowiedź MIla− |x−y|≤1 ⇔i |y−x|≤1 udowadniam z własności wart. bezwzględnej, tak? b)S⊂R², (x.y)∊S: |x|=|y| c) S⊂R² (x,y)∊S (x−y)(x+y)=0

Basiek: Masakra... ta tabelka jest dość ciekawa, ale praktyczna tylko w przypadku, gdy zbiór jest określony na liczbach. Ale rozgryzę, może się przyda, dziękuję. AC− dzięki. A Ty Mila jesteś nieoceniona.

Basiek: A swoją drogą− czy to, że relacja jest symetryczna, automatycznie skreśla antysymetryczność?

Mila: Tak |x−y|=|y−x| własność | | i nic nie trzeba więcej . b) 1)Zwrotność (x,x)∊S ⇔|x|=|x| tak , relacja zwrotna 2) symetryczność (x,y)∊S⇔(y,x)∊S ? |x|=|y|⇔|y|=|x| relacja symetryczna ( |x|−|y|=0⇔|y|−|x|=0⇒|y|=|x|) 3) przechodniość (x,y)∊S i (y,z)∊S⇔(x,z)∊S ? |x|=|y| i |y|=|z|⇔|x|=|z| relacja przechodnia bo |x|−|y|=0 i |y|−|z|=0 po dodaniu stronamix|−|y|+ |y|−|z|=0 ⇔|x|−|z| =0⇔|x|=|z|

Basiek: Okej, a jeszcze do tego d) spójność ? Dochodzimy do |x−y|≤1 ⋁ |y−x|≤1 korzystając z tej samej własności: |x−y|=|y−x|, więc zapisuję tylko |x−y|≤1 kontrprzykład: dla x=2,5 , y=2 To jest dobrze?

Basiek: Oczywiście kontrprzykład ma być kontr, a nie udowadniać, np. x=5, y=2 (?)

Mila: Trochę mi wiedza wyparowała. Tak myślałam, że AC pomoże. c)S⊂R² (x,y)∊S ⇔(x−y)(x+y)=0 1) zwrotność (x,x)∊S⇔(x−x)(x+x)=0 tak, relacja zwrotna 2) symetryczność (x,y)∊S⇔(y,x)∊S (x−y)(x+y)=0⇔(y−x)(y+x)=0 tak, jeśli (x−y) =0 to (y−x) =0 i iloczyn równy 0. jeśli x+y=0 to y+x=0 relacja symetryczna 3) przechodniość (x,y)∊S i (y,z)∊S⇔(x,z)∊S (x−y)(x+y)=0 i (y−z)(y+z)=0⇔(x−z)(x+z)=0 tak, bo x²−y²=0 y²−z²=0 po dodaniu x²−z²=0⇔(x−z)(x+z)=0 cnw Dobranoc.

Basiek: Mila− ogromnie Ci dziękuję. Teraz przynajmniej wiem, co trzeba gdzie podstawić. Będę kombinować. Link też bardzo się przyda. Dobranoc.

Mila: JUtro przeczytam resztę.Czytaj teorię.

Basiek: Ja będę dopiero... w następny piątek. Właśnie w tym problem mój tkwi. W mieszkaniu nie mam internetu... Ale i tak bardzo, bardzo, bardzo mi pomogłaś. No i przepraszam, że tak to wyglądało− że musiałaś robić za mnie wszystko.