wartość Paweł: jak naszkicować taką funkcję : f(x) = ||1−x | − 3 | − chodzi mi o to że są 2 wartości bezwzględne

loitzl9006: 1) rysujesz |x| 2) przesuwasz 1) o wektor [1;0] i dostajesz w ten sposób |x−1| 3) korzystasz z własności |a−b|=|b−a| czyli z tego wynika że |x−1|=|1−x| 4) przesuwasz |1−x| o wektor [0;−3] i dostajesz |1−x|−3 5) tą część wykresu, która znajduje się pod osią iksów, odbijasz symetrycznie względem osi x, dostajesz f(x).

Saizou : 1− rysujesz 1−x 2− nakładasz na nią wartość bezwzględną l1−xl 3− przesuwasz o 3 jed. w dół lx−1l−3 4− nakładasz moduł wartości bezwzględnej ll1−xl−3l

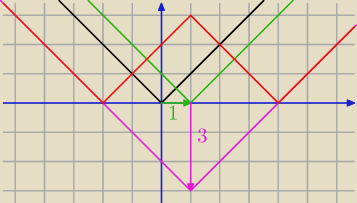
ZKS: ||1 − x| − 3| = ||x − 1| − 3| y = |x| y = |x − 1| y = |x − 1| − 3 y = ||x − 1| − 3|

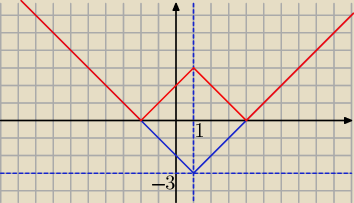
Gustlik: Można krócej: zasada y=f(x−p)+q − przesuwamy funkcję f(x) o wektor [p, q]. y=||x−1|−3| Najpierw narysujemy funkcję y=|x−1|−3, czyli y=|x| i przesuwamy o wektor [1, −3], bo p=1, q=−3. 1. Rysujesz pionową prostą przecinającą oś OX w punkcie p=1 (prosta x=1) i poziomą przecinająca oś OY w punkcie q=−3 (prosta y=−3), traktujesz te nowe osie (linie przerywane) jak nowy układ współrzędnych i rysujesz w nim funkcję y=|x| − otrzymujesz w ten sposób wykres y=|x−1|−3. 2. Odbijasz ujemną (czyli dolną) część tego wykresu na górę (tak jakbys zginał kartkę wzdłuż osi OX i dolną część kartki zagiął na górę) i otrzymujesz wykres y=||x−1|−3|.