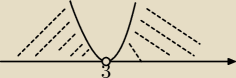
Proszę o sprawdzenia zadania Ola: Witam! Prosze o sprawdzenia zadania: ^4−x_x−5>¹_1−x D=R\{1,5} ^4−x_x−5 − ¹_1−x>0 ^{(4−x)(1−x)}_{(x−5)(1−x)} − ^x−5_{9x−5)(1−x)}>0 u{(4−x)(1−x) − (x−5)}{(x−5)(1−x)>0 u{x²−6x+9}{(x−5)(1−x)>0 (x²−6x+9)(x−5)(1+x)>0 delta= x₀=3 x należy (−nies.;3)u(3;+nies.)

sushi_gg6397228: zwieksz troche czcionke przez U jako ulamek

Ola:

(4−x)(1−x)		x−5
	−		>0
(x−5)(1−x)		(x−5)(1−x)

(4−x)(1−x) − (x−5)
	>0
(x−5)(1−x)

x2 − 6x +9
	>0
(x−5)(1−x)

(x² − 6x+9)(x−5)(1−x) delta= 0 x₀=3

Ola:

(4−x)(1−x)		x−5
	−		>0
(x−5)(1−x)		(x−5)(1−x)

(4−x)(1−x) − (x−5)
	>0
(x−5)(1−x)

x2 − 6x +9
	>0
(x−5)(1−x)

(x² − 6x+9)(x−5)(1−x) delta= 0 x₀=3

sushi_gg6397228: mamy az 3 miejsca zerowe−−−> wiec bedzie fala

PuRXUTM: sushi ale założenia, nie pamiętam jak to do końca było więc nie będę pisał żeby nie wprowadzać w błąd

PuRXUTM: wydaje mi się że rozwiązaniem jest x∊R\{3}

sushi_gg6397228: https://matematykaszkolna.pl/strona/183.html

	(...)(...)
czytaj od miejsca		<0
	(....)(....)

Ola: ale dlaczego "fala", skoro 1i 5 nie wchodzą w "skład" dziedziny?

sushi_gg6397228: beda mieć kółka otwarte ( my musimy znaleść tylko znak)

PuRXUTM: no rzeczywiście przepraszam za wprowadzenie w błąd

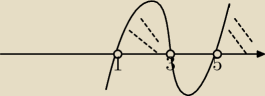
Ola: tak? x∊(1;3)u(5;+nies.)