Wartość bezwzględna
Franki: Witam , bardzo prosze o pomoc z tym przykładem bo nie wiem jak go ugryźć
|2x+5|+|x|+8=3√x2−2x+1
13 paź 18:48
PuRXUTM: √x2−2x+1=√(x−1)2=Ix−1I
13 paź 18:53
Eta:
x2−2x+1= (x+1)2 √a2= |a|
|2x+5|+|x|+8= 3|x−1| , miejsca zerowe pod modułami: x= −2,5 , x= 0, x= 1
teraz rozwiąż w przedziałach
1o dla x€ ( −∞; −2,5)
2o dla x€ <2,5;,0)
3o dla x€ <0,1)
4o dla x€ <1,∞)
13 paź 18:54
13 paź 18:55
Franki: Okej rozumiem , teraz robię to w tabelce , jednak że mam takie pytanie. |2x+5| w pierwszym
przedziale czyli ( −∞; −2,5) pozostaje takie same czy zmieniamy znaki , czyli na −2x−5 , jak
nie to w ktorym przedziale . Jest na to jakaś reguła albo wytłumaczenie bo zawsze w tym
momencie się mylę i nie wiem dla ktorej wartości bewzględnej zmienić znak w danym przedziale
13 paź 19:01
13 paź 19:03
Eta:
Jeżeli "jesteś " po lewej stronie miejsca zerowego → zmiana znaków
po prawej stronie miejsca zerowego → bez zmiany znaków
13 paź 19:04
PuRXUTM: wybierasz jakąś liczbę z tego przedziału np. −10 i podstawiasz i patrzysz czy wyrażenie jest
ujemne czy dodatnie

13 paź 19:05
Franki: w przedziale ( −∞; −2,5) odpowiedz to x=−2?
13 paź 19:05
Eta:
I bardzo dobrze Was uczył

Ja wskazałam Ci jedynie przedziały .
13 paź 19:05
Eta:
w przedziale (−∞;−2,5)
−2x−5−x+8= −3x+3 ⇒ 3=3 −−−−− nieskończenie wiele rozwiązań z przedziału x€(−∞;−2,5)
13 paź 19:09
Franki: w przedziale <−2,5;,0)
2x+5−x+8=−3x+3 ⇒ x=−2,5
13 paź 19:13
Eta:
ok

13 paź 19:14
Franki: W końcu to zajarzyłem xd jaka radość

13 paź 19:16
Eta:

w nagrodę

13 paź 19:17
Franki: | | 2 | |
2x+5+x+8=−3x+3 ⇒ 6x=−10 ⇒ x=−1 |
| |
| | 3 | |
13 paź 19:19
Franki: dam róże xd

13 paź 19:20
Franki: w ostatnim wyjdzie 13=3 czyli nie skonczenie wiele rozwiązań z przedziału <1,∞)
13 paź 19:22
Eta:

| | 2 | |
3/ x= −1 |
| ∉ (<0,1) −−−−−− więc nie jest rozwiązaniem |
| | 3 | |
4/ 13= 3 −−−−−−− sprzeczność ( czyli brak rozwiązań !
13 paź 19:30
Eta:
Teraz dostajesz ........
figę z makiem 
13 paź 19:31
Franki: aha czyli jak jest 3=3 to wtedy nie skończona liczba rozwiązań rozumiem
a jak mam na przykład ||x|−1|≤2 to :
x−1≤ 2 v x−1≤ −2
albo:
x ≤ 3 v x ≤ −1

13 paź 19:35
Krzysiek : Franki jezeli tego nie rozumiesz to to nalepiej widac jak narysujesz sobie os liczbowa i
przedzialy Wtedy widzisz kiredy zmienic znak lub nie . Jesli jednak i tego nie rozumiesz to
wezmy jako przyklad ta wartosc bezwzglena I2x+5I i przedzial (−∞,−2,5) Troche to dluzej trwa
bo trzeba sobie policzyc ale jest ok. W\WEz sobie jakas liczbe z tego przedzialu (−∞,−2,5) np
(−3)i podstaw ja za x do wartosci bezwzglednej
Mamy I2x+5I=I2*(−3)+5I=I−1I Pod wartoscia bezwgledna wyszlo minus wiec nalezy zmienic znak
opuszczajac wartosc bezwzgledna ⇒I2x+5I=−(2x+5)=−2x−5 .
Teraz zmienmy przedzial np <0,15) to teraz zobaczmy czy bedziemy musieli zmieniac znak .
Bierzemy przykladowa liczbe z tego przedzialu powiedzmy 4 i za x wstawmy 4 do wartosci
bezwzglednej to liczymy I2x+5I=I2*4+5I=I13I dodatnie wiec znaku nie zmieniamy opuszczajac
wartosc bezwzgledna ⇒I2x+5I= 2x=5. Mysle ze teraz bedziesz wiedzial czy zmieniac znak czy nie
dopoki nie bedziesz to robil szybciej patrzac na os i wyznaczone przedzialy
13 paź 19:35
Franki:
Eta:
Teraz dostajesz ........figę z makiem

poprawie się obiecuje xd
13 paź 19:36
Franki: Dzięki Krzysiek właśnie na to naprowadziła mnie Eta i PuRXUTM i zaczynam to ogarniać jako tako
xd
13 paź 19:39
Eta:
I
Krzysiek się "wciął" ze swoim "wypracowaniem"

13 paź 19:39
Franki: Kurde w odpowiedziach mi wszyło <−3 ,3 > ale nie mam pojęcia dlaczego

13 paź 19:41
Eta:
Przeczytaj moje krótkie wyjaśnienie z 19:04
13 paź 19:42
Eta:
Sprawdź, czy dobrze napisałeś równanie .
13 paź 19:44
13 paź 19:48
Eta:
Achh

chodzi Ci o nierówność! ( myślałam,że o poprzednie równanie)
||x|−1| ≤2
|x|−1 ≤ 2 i |x|−1≥ −2
|x|≤3 i |x| ≥ −1 ⇒x€R
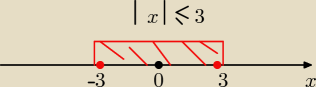
|x|≤3 ⇒ x≤ 3 i x≤ −3 ⇒ x€ < −3, 3>
13 paź 19:52
Franki: Chyba ze to ma być tak:
x−1≤ 2 v x+1≤ −2
x ≤ 3 v x ≤ −3
Tylko skąd by się + znalazł przy tej jedynce

13 paź 19:53
Eta:
Już jasne?

13 paź 19:55
Franki: Aha okej rozumiem już ,tylko czemu wykluczamy |x| ≥ −1?
13 paź 19:55
Eta:
Bo bezwzględna wartość z liczby zawsze ≥0 czyli jest > −1
13 paź 19:57
Franki: a nooo takk a w tym x ≤ 3 v x ≤ −3 , znak przy −3 będzie zawsze w tą stronę co 3 ? Także w
innych przykładach z nierównoscią

?
13 paź 20:00
Eta:
Nie, tam wkradł mi się chochlik (sorry)
|x|≤ 3 ⇒ x≤3 i x ≥ −3
13 paź 20:02
Franki: Dziękuje bardzo za pomoc , teraz sprobuje sam ogarnąć parę przykładów jak czegoś nie bedę
wiedział to będę pisał xdd
13 paź 20:04
Eta:
13 paź 20:05
Krzysiek : Czesc Eta. jak pisalem to jeszce nie bylo waszych postow . Ale jak wyslalem to sie za glowe
zlapalem co narobilem
13 paź 21:24

 Ja wskazałam Ci jedynie przedziały .
Ja wskazałam Ci jedynie przedziały .


 w nagrodę
w nagrodę 




 poprawie się obiecuje xd
poprawie się obiecuje xd


 nawet rozwiązuje ten przykłąd analogicznie do tego https://matematykaszkolna.pl/strona/1106.html
nawet rozwiązuje ten przykłąd analogicznie do tego https://matematykaszkolna.pl/strona/1106.html
 chodzi Ci o nierówność! ( myślałam,że o poprzednie równanie)
||x|−1| ≤2
|x|−1 ≤ 2 i |x|−1≥ −2
|x|≤3 i |x| ≥ −1 ⇒x€R
|x|≤3 ⇒ x≤ 3 i x≤ −3 ⇒ x€ < −3, 3>
chodzi Ci o nierówność! ( myślałam,że o poprzednie równanie)
||x|−1| ≤2
|x|−1 ≤ 2 i |x|−1≥ −2
|x|≤3 i |x| ≥ −1 ⇒x€R
|x|≤3 ⇒ x≤ 3 i x≤ −3 ⇒ x€ < −3, 3>


 ?
?
