obliczanie zbioru wartosci funkcji jey47s:

	x
1) Dana jest funkcja: f(x)=		, gdzie x∊R\{−2,2}. Wykaż że zbiorem wartosci tej funkcji
	4−x2

jest zbiór liczb rzeczywistych. 2) Wyznacz zbiór wartości funkcji f(x)=5−sin²x, gdzie x∊R. 3)Wykaż że w szescianie, odległość krawędzi od nieprzecinajacej sie z nią przekątnej sześcianu jest równa połowie długości przekątnej ściany. i może troche glupie pytanie, czy √(a²)=|a|, czy po prostu samo a? jezeli chodzi o dwa pierwsze zadania to wydaje mi sie ze umiem je rozwiazac, ale chodzi mi tu o ogolna metode jak wyznacza sie zbior wartosci danej funkcji. z góry dzieki za pomoc

Mickej: wow widziałem takie cudo Skoro funkcja ma mieć zbiór wartosci całe R to

x
	=a musi mieć rozwiązanie dla każdego a∊R
4−x2

x
	−a=0
4−x2

ax2+x−4a
	=0 ułamek =0 gdy licznik równy 0 czyli
4−x2

ax²+x−4a=0 rozpatrujemy 2 przypadki 1. a=0 wtedy otrzymyjemy postać x=0 czyli jest rozwiązanie 2. a≠0 Δ=1+16a² a to zawsze większe od 0 czyli zawsze ma rozwiązanie więc

x
	przyjmuję wszystkie wartosci rzeczywiste
4−x2

Mickej: co do 2 zadania to na podstawie wykresu lub podstawiając pod sinx=t i ograniczyć t∊<−1;1> zbiór to oczywiscie <4;5>

Mickej: √a²=|a|

jey47s: dzeki wielkie za pomoc

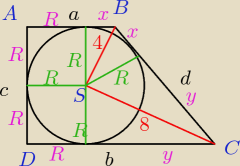
jey47s: mam jeszcze problem z takim zadaniem: środek okregu wpisanego w trapez prostokątny znajduje sie w odleglosci 4 oraz 8 od dluzszego ramienia trapezu. Oblicz pole tego trojkata. Rysunek jest moj, jezeli mialbym pewnośc że trojkat BSC jest prostokątny, to zadanie byloby juz do rozwiazania, ale takiej pewnosci nie mam wiec prosze o pomoc mam nadzieje ze widac cos z tego rysunku

Bogdan: Było już kilka razy, zobacz np. tu 15671

jey47s: dalem juz sobie rade jakos, ale dzieki za pomoc, zadanie jest banalnie proste jesli sie cos zauwazy i na cos wpadnie