obliczyć wyniki liczb zespolonych
mar: 3√i √i √−i i5 i8 3√−i (1+√3i)12 POMOŻE mi ktoś
rozwiązać te wyniki ?
13 paź 16:05
ZKS:
z = i /
8
z
8 = i
8
(z
4 − i
4)(z
4 + i
4) = 0
(z − i)(z + i)(z
2 + i
2)(z
4 + i
4) = 0
(z − i)(z + i)(z
2 − 1)(z
4 − i
2) = 0
(z − i)(z + i)(z − 1)(z + 1)(z
2 − i)(z
2 + i) = 0
| | 1 + i | |
z2 = i ⇒ z = ±√i ⇒ z = ± |
| |
| | √2 | |
| | 1 − i | |
z2 = −i ⇒ z = ±√−i ⇒ z = ± |
| |
| | √2 | |
| | 1 + i | | 1 − i | |
z = ±i ∨ z = ±1 ∨ z = ± |
| ∨ z = ± |
| |
| | √2 | | √2 | |
13 paź 16:12
mar: a ten
√−i jak należy zrobić

13 paź 16:45
Mila:
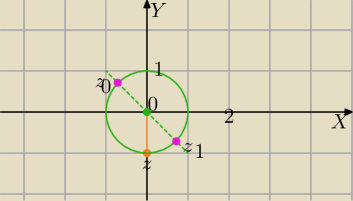
z=−i=0−1i
|z|=1
| | φ+2kπ | | φ+2kπ | |
√z=√1*(cos |
| +i*sin |
| ) k∊{0,1} |
| | 2 | | 2 | |
| | | | | | √2 | | √2 | |
z0=(cos |
| +i*sin |
| )=− |
| + |
| i |
| | 2 | | 2 | | 2 | | 2 | |
| | | | | | 7π | | 7π | |
z1=(cos |
| +i*sin |
| )=cos |
| +isin |
| |
| | 2 | | 2 | | 4 | | 4 | |
Algebraicznie
√−i=x+iy ⇔(x+iy)
2=−i x,y∊R
x
2+2xyi−y
2=−i
(x
2−y
2)+2xyi=−i
x
2−y
2=0 i 2xy=−1
(x−y)(x+y)=0 i 2xy=−1
rozwiąż w zbiorze R
13 paź 21:28
Mila:
i5=i2*i2*i=(−1)*(−1)*i=i
i8=(i2)4=(−1)4=1
13 paź 21:32

 z=−i=0−1i
|z|=1
z=−i=0−1i
|z|=1