Dane są funkcje kate09: Dane sa funkcje f(x)=x²+6x, g(x)=5x. Rozwiązać równanie: f(x)=ig(x)I a)analitycznie, b)graficznie

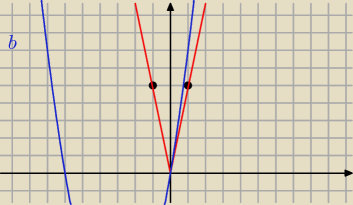
Aga1.: W jednym układzie współrzędnych sporządzasz wykres funkcji y=I5xI −−kolor czerwony i y=x²+6x−−−kolor niebieski Punkt wspólny (0,0) odp.x=0 a) x²+6x=I5xI Gdy x≥0 x²+6x=5x dokończ Gdy x<0 x²+6x=−5x dokończ

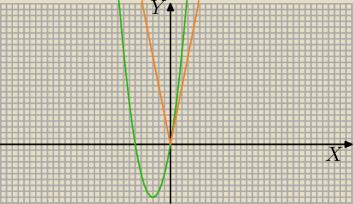
Mila: a) x²+6x=|5x| x≥0 x²+6x=5x x²+x=0⇔ x(x+1)=0⇔ x=0 lub x=−1 ∉D x<0 x²+6x=−5x x²+11x=0 ⇔x(x+11)=0 x=0 lub x=−11 Odp. x=0 lub x=−11 b)Nie widać przecięcia na lewej gałązce paraboli, w zeszycie Ci wyjdzie

Krzysiek : Kate 09. Kolezanki Aga i Mila napisaly X²+6x=I5xI i pozniej x²+6x=5x dla x≥0 i x²+6x=−5x dla x<0 czy wiesz dlaczego ? jesli nie to jedna z wlasnosci wartosci bezwzgleednej jest taka Ia*xI=aIxI dla a≥0 Wobec tego nasza funkcje Ig(x)Izapiszemy I5xI=5IxI i mamy dla x≥0 IxI=x czyli x²+6x=I5x I=x²+6x=5IxI=x²+6x=5x i rozwiaz to rownanie Dla x<0 IxI=−x czyli nasze x²+6x=I5xI=x²+6x=5IxI=x²+6x=5*(−x)=x²+6x=−5x i prosze teraz to rozwiazac algebraicznie te rownania . Rysuniki juz CI Aga 1 i MIla narysowaly.