Pomocyyy! :D Sławomir: Trudna funkcja: f(x) = { 2 − x , |x| ≥ −2 2 − |x| , |x| <2 Jak to rozwalić? Pozdrawiam!

Sławomir: a z tym ktos jest mi w stanie pomóc?

Sławomir: naprawde nikt?

Sławomir: haaaaalo

Aga1.: A nie powinno być IxI≥2 zamiast IxI≥−2?

Sławomir: oj tak, chyba masz racje. Zapomnialem, ze tam jest błąd.

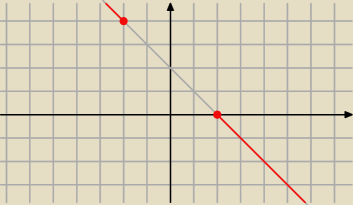
Aga1.: 1)y=2−x, gdy x≤−2 lub x≥2

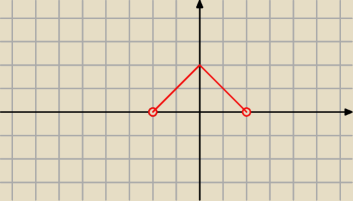
Aga1.: 2) y=−IxI+2, gdy x∊(−2,2)

Aga1.: Teraz wykresy czerwone narysuj na jednym układzie współrzędnych.

Sławomir: ok. ale moglabys mi wytlumaczyc jak do tego doszłaś? W tym pierwszym przykładzie jak CI się udało napisać to: gdy x≤−2 lub gdy x≥2 a w tym drugim tez niewiem jak to sie udalo rozpisac. Bo ja slabo kumam wartosc bezwzgledna, stad te problemy pewnie...

Aga1.: Rozwiązałam nierówności 1)IxI≥2 x≥2 lub x≤−2 2) IxI<1 x<2 i x>−2 Wyznaczam część wspólną i x∊(−2,2)

Sławomir: rozuuumiem! Dziękujeeee! A jest jakiś inny sposób wyznaczania części wspólnej jak tylko poprzez narysowanie sobie tego na osi?

Aga1.: Jest. np. IxI<1⇔−1<x<1, czyli x∊(−1,1)

Sławomir: aha jeszcze jedno. W tym drugim jest: 2− |x| i tego nie kumam. Co z tą wartosci bezwzględną? Bo rozumiem, ze to bedzie miało sens dla x<2 i x > − 2 ale co nam zmieni?

Sławomir: Dobra, już nie tłumacz kumam

Sławomir: Ostatnią rzecz mi powiedz, to jak to narysowac na osi, skoro jedno kółeczki jest zamalowane a drugie nie zamalowane a one nachodzą na siebie?

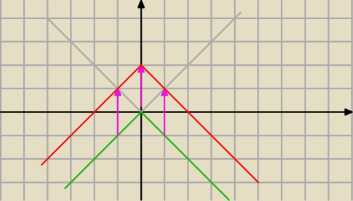
Aga1.: y=2−IxI Narysuję Ci dla x∊R y=IxI kolor szary y=−IxI koloru zielonego (symetria względem osi 0x.) y=−IxI+2 wykres zielony przesunięty o 2 jednostki do góry i masz wykres czerwony.

Aga1.: Jak rysujesz obydwa wykresy na jednym układzie współrzędnych to otrzymujesz wykres końcowy będący sumą tych dwóch. Odp. na ostatnie Twoje pytanie. Otrzymasz kółeczko zamalowane.

Sławomir: ok, ten przykład trudny, bo trudny − ale rozumiem. Chciałbym Ci serdecznie podziękować Bardzo doceniam Twoje trudy, żeby mi to wytłumaczyć

Aga1.: ok.