parametr Mati_gg9225535: Dla jakich wartości parametru m∊R równanie (m−304^|x|−2m+1=0 ma dwa różne rozwiązania?

Mati_gg9225535: oj nawias nie wyszedł jeszcze raz: (m−3)4^|x|−2m+1=0

Mati_gg9225535: w ogole nie widze tu równania z którego moglbym wyliczyć dwa rozwiązania, co najwyżej jedno

Bogdan:

	2m − 1
4|x| =		dla m≠3,
	m − 3

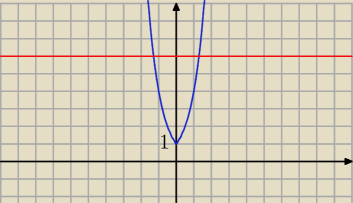
y = 4^|x| wykres przekształconej funkcji wykładniczej (niebieski wykres)

	2m − 1
y =		wykres funkcji stałej (czerwony wykres)
	m − 3

	2m − 1
Równanie ma dwa różne rozwiązania dla		> 1 i m≠3
	m − 3

Mati_gg9225535: a no tak bo to sie tak robilo dzieeeeeeki wielkie

Bogdan:

Bogdan: Trzeba jeszcze dokończyć i rozwiązać nierówność z parametrem m

Mati_gg9225535: tak tak, z tym sobie juz poradze chodzilo mi tylko o metode wlasnie, to tylko graficznie da sie zrobic ?

Bogdan: Nie rozwiązujemy przecież tego zadania graficznie, rysunek jest tu ilustracją problemu. Trzeba jednak stwierdzić, że krzywa y = 4^|x| jest wykresem funkcji wykładniczej y = 4^−x dla x < 0 lub wykresem funkcji y = 4^x dl x ≥ 0, krzywa y = 4^|x| ma najmniejszą wartość równą 1 dla x = 0 i jej ramiona są skierowane do góry.

Mati_gg9225535: no fakt, ale jesli naszkicuje rysunek funkcji f(x)=4^|x| to moge pomnac zalozenia ze dla x≥0 coś tam dla x<0 coś tam, prawda? i od razu przejsc do nierówności

Bogdan: Ja uznałbym takie rozwiązanie z rysunkiem

Mati_gg9225535: ok dzieki za pomoc