nierownosc wymierna z wartoscia bezwzgledna uki: Jak takie cos zrobic? Moze ktos rozpisac?

	2x−3
|		|≥2
	x+1

Jolanta:

2x−3		2x−3
	≥ 2 lub		≤ −2 x+1≠0
x+3		x+1

x≠−1

Jolanta: x+3≠0 x≠−3

ZKS: Zał. x ≠ −1

	2x − 3
|		| ≥ 2 / * |x + 1|
	x + 1

|2x − 3| ≥ 2|x + 1| 2x − 3 ≥ 2x + 2 ∨ 2x − 3 ≤ −2x − 2

Jolanta:

2x−3
	−2≥0
x+3

2x−3−2(x+3)
	≥0
x+3

2x−3−2x−6
	≥ 0
2x+3

−9
	≥0
2x+3

licznik jest ujemny czyli wynik moze być dodatni jeżeli mianownik też jest ujemny 2x+3 <0 2x<−3 x<−1,5 Równy 0 nie moze byc skoro licznik jest −9 a mianownik nie moze być 0 Wszystko rozumiesz ?

ZKS: Ale w mianowniku jest x + 1?

Jolanta: Oj nie wiem jak mi sie tak poplątało w mianowniku x+1 a nie x+3

pigor: ... , proponuję np. tak :

	2x−3		|2x−3|
|		|≥2 ⇔		|≥2 /*|x+1| i x+1≠0 ⇔ |2x−3|≥2|x+1| /2 i [c[x≠ −1] ⇒
	x+1		|x+1|

⇒ (2x−3)² ≥4(x+1)² ⇔ 4x²−12x+9 ≥ 4x²+8x+4 ⇔ 5 ≥ 20x i x≠ −1 ⇔ ⇔ x ≤ ¹₄ i x≠ −1 ⇔ x∊(−∞;−1) U (−1; ¹₄> . ...

Jolanta:

	2x−3
U{2x−3}{x+1 ]≥2 lub		≤−2 x≠−1
	x+1

2x−3−2(x+1)		2x−3+2(x+1)
	≥0		≤0
x+1		x+1

2x−3−2x−2
	≥0 U2x−3+2x+2}[x+1} ≤0
x+1

−5		4x−1
	≥0		≤0
x+1		x+1

x+1<0 (4x−1)(x+1)≤0

	−1
x<−1 x=		(4x−1)(x+1)=0
	4

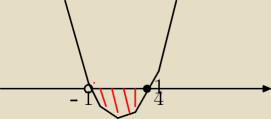Jolanta: (4x−1)(x+1) <0 dla x∊(−1,U{1}[4}> teraz wszysko dodajemy

	1`
x∊(−∞ −1) v(−1,
	4

Jeżeli w zadaniu bEdzie znak < np |x+3| <4 to rozwiazaniem nie będzie suma przedziąłow tylko cześc wspólna