teoria ciągu gigi: Witam mam kłopot ze zrozumieniem teorii a mianowicie: ⋁_ε>0 (dla każdego epsilon) ∧_N (istnieje N− liczba naturalna) ⋁_n≥N (dla każdego n− (tu chyba nr wyrazu ciągu) ) Mam tez rysunek w którym mam wykres granicy względem epsilon: ε−g<a_n<ε+g Głównie nurtuje mnie ten epsilon co to właściwie jest? To wynik konkretnego wyrazu czy jak? Byłbym wdzięczny jeśli ktoś w miare prostym językiem powie o co w tym chodzi.

pilne: czy to czesc wykladu z PK mech?

Krzysiek: dla każdego ε> 0 dobierzemy takie N, że dla n≥N wszystkie wyrazy tego ciągu będą zawierać się w przedziale: (g−ε,g+ε) Czyli po 'polsku' prawie wszystkie wyrazy ciągu muszą zawierać się w pewnym przedziale nie ważne czy dopiero od a₃ czy od a₁₀₀₀₀ ciąg będzie się zawierał w tym przedziale 'prawie wszystkie' wyrazy ciągu oznacza, że od pewnego miejsca.

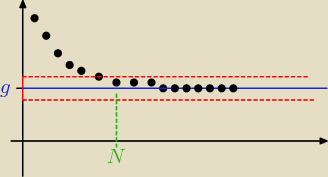
Andrzej: g oznacza granicę ciągu czerwona górna linia jest na wysokości g+ε, dolna g−ε utworzył się zatem taki "pasek" między czerwonymi liniami. Szerokość tego paska to 2ε. i teraz tłumaczę z polskiego na nasze: dla każdego ε>0 wszystko jedno jak szeroki / wąski będzie mój pasek istnieje N naturalne to jest takie miejsce dla każdego n ≥ N że począwszy od tego miejsca g−ε < a_n < g+ε wszystkie kropki leżą wewnątrz paska

Godzio: ∀_ε>0 ∃_N∊ℕ ∀_{n ≥ N} |a_n − g| < ε Teraz słownie: Dla każdego dowolnie małego epsilona, istnieje takie miejsce N, że dla każdego n większego od N wszystkie wyrazy ciągu a_n są dostatecznie blisko granicy g. Co to wszystko oznacza ? Oznacza to tyle, że jeżeli idziemy sobie wyrazami: a₁,a₂,... to dojdziemy w końcu do takiego wyrazu a_N, że następne wyrazy, czyli a_N+1, a_N+2, ... będą blisko granicy, a ich odległość od niej będzie mniejsza od ε. Epsilon to dowolnie mała liczba.

gigi: Dzięki wielkie, patrze się na te znaki od 2 dni i niby wiem jak je przeczytać ale nie ułożyłbym z nich takiej teorii