liczby zespolone jacek: Liczby zespolone Wyznacz ℛ(w + z), im(w + z) [urojona], ℛ(zw), im(zw). Gdzie z = a + bi oraz w = c + di * zw = (a + bi)(c + di) = ac + adi + cbi − bd = (ac − bd) + (ad + cb)i a) ℛ(z + w) = ℛ(a + bi + c + di) = ℛ( (a + b) + (b + d)i ) = a + b b) im(z + w) = im(a + bi + c + di) = im( (a + b) + (b + d)i ) = b + d c) ℛ(zw) = ℛ( (ac − bd) + (ad + cb)i ) = ac − bd d) im(zw) = im( (ac − bd) + (ad + cb)i ) = ad + cb Dobrze to zrobiłem? Jeżeli ktoś mógłby wytłumaczyć o co chodzi tutaj: Wyznacz wszystkie liczby zespolone iⁿ, n∊ℕ.

Krzysiek: a) a+c iⁿ policz: i¹ ,i² ,i³ ,i⁴ ,i⁵ ,i⁶ spróbuj coś zauważyć

jacek: nie widze nic prócz tego, że: i, −1, i, −1, i, −1 czyli a,b,c,d dobrze w 1 zadaniu ?

Krzysiek: b,c,d, ok 2) i³ =−i i⁴ =(−1)² =1 i¹ =i⁵ i² =i⁶ i³ =−i i⁷ =(i³ )(i³ )i =−i =i³ zatem: i^4m+1 =i i^4m+2 =−1 ...

jacek: no tak to rozumiem ale co mamy dokładnie wyznaczyć? sam próbuję uczyć się zespolonych więc niektóre pytania mogą wydawać się idiotyczne

Krzysiek: chodzi o to, że co 4 potęga liczby się powtarzają więc gdy n=4m+1 czyli gdy potęga jest równa: 1,5,9,... to: iⁿ =i^4m+1 =i gdy n=4m+2 (2,6,10,...) to: iⁿ =i^4m+2 =−1 gdy n=4m+3 i^4m+3 =−i gdy n=4m+4 i^4m+4 =1 m∊N innej postaci 'n' już nie będzie

jacek: Czyli chodziło o napisanie tych 4 warunków? W sumie to logiczne.

Krzysiek: tak, możesz np.zapisać za pomocą klamry: | i ,gdy n=4m+1 iⁿ =| | | (oczywiście tu tej klamry nie napiszę )

jacek: dziękuję pięnie lecz jeszcze jedno pytanie się nasuwa, jak narysować na płaszczyźnie |z + 3i| < 1 oraz |z + 4 − 2i| ≤ 3.

Krzysiek: z+3i=x+yi+3i=x+i(y+3) |x+i(y+3)| =√x² +(y+3)² zatem: √x² +(y+3)² <1 / ² x² +(y+3)² <1 −równanie koła

jacek: w każdym wypadku tak postępujemy, że za z podstawiamy x i y? np.: z + 4 − 2i = x + yi + 4 − 2i = x + (y − 2)i + 4 ?

Krzysiek: tak bo potem liczysz moduł

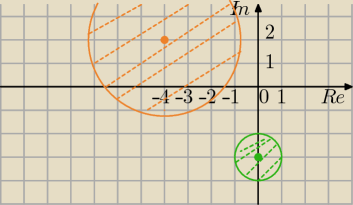
Mila: Korzystamy z interpretacji geometrycznej. a) |z+3i|<1⇔|z−(−3i)|<1 koło o srodku (0;−3) i promieniu 1 bez brzegu. b) |z + 4 − 2i| ≤ 3.⇔|z−(−4+2i)|≤3 koło o środku (−4,2) i promieniu 3