Zbadaj liczbę rozwiązań równania ze względu na wartość parametru m −x^2+2|x|=m^2 Ola.: Zbadaj liczbę rozwiązań równania ze względu na wartość parametru m −x²+2|x|=m²−2. Plus do tego narysować wykres y=g(m) Bardzo proszę o pomoc ! Siedzę z tym już kilka godzin i nie umiem. Jeśli ktoś ma ochotę zrobić to proszę o dokładne napisanie wszystkiego krok po kroku

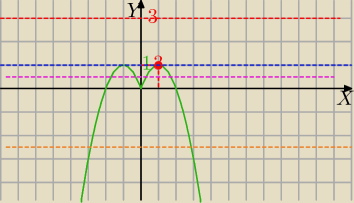
Mila: 1) rysujesz wykres funkcji f(x)=−x²+2|x| obliczas największą wartość funkcji y=−x²+2x

	−2
xw=		=1
	2*(−1)

y=1 2) rozważasz funkcje stałe y=m²−2 dla różnych wartości [np.y=4 ta prosta nie przecina wykresu f(x) brak rozwiązań] a) dla m²−1>1 brak rozwiązań (czerwona prosta) b) dla m²−2=1 są dwa rozwiązania (niebieska prosta) c) dla m²−2>0 m²−2<1 są 4 rozwiązania ( np. różowa prosta) d) dla m²−2=0 są 3 rozwiązania (oś OX) e)dla m²−2<0 są dwa rozwiązania (np. pomarańczowa prosta) rozwiąż te warunki a,b,c,d,e to narysujemy wykres g(m)

Ola.: Nie wiem czy dobrze wgl to liczę, ale wyszło mi, że: a) m∊∅ b) m=√3 c) m>√2 ⋀ m<√3 d) m=√2 e) m<√2

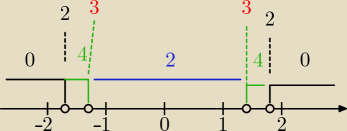
Mila: a) m²−2>1⇔m²−3>0 (tam była literówka)⇔ (m−√3)(m+√3)>0⇔m<−√3 lub m>√3 0 rozwiązań b)m²−2=1⇔m=√3 lub m=−√3 2 rozw. c)m²−2<1 i m²−2>0⇔ m∊(−√3;−√2 ) lub m∊(√2;√3) 4 rozw. d)m²−2=0⇔m=√2 lub m=−√2 3 rozw. e)m²−2<0 ⇔m∊(−√2;√2) 2 rozw. przy nierównościach kwadratowych rysuj parabolę. Teraz narysuj wykres g(m). U góry masz napisane wartości funkcji g(m)

Ola.: Dziękuję bardzo, już mniej więcej wiem, jak to zrobić

Mila: