homograficzna
minikóper: Jak narysować wykresy funkcji
W a) poradziłem sobie tak:
D=R/{1}
| | −x | |
x∊(−∞, 0) ⇒ f(x) = |
| dostałem homograficzną i ją narysowałem |
| | x−1 | |
| | x | |
x∊(0, +∞) ⇒ f(x) = |
| też narysowałem dostalem |
| | x−1 | |
z tego dostałem dwie hiperbole, a później patrzylem jakie wartosci przyjmuje funkcja f(x) w
przedzialach x∊(−
∞, 1) i x∊(1, +
∞)
dla pierwszego f(x)<0 dla drugiego f(x)>0 wiec pozaznaczalem te czesi ktore temu odpowiadaja i
wyszlo dobrze. pytanie tylko czy b) tez tak robic?
11 paź 16:57
minikóper: moglby ktos tylko zerknac? bo nauczyciel powiedzial ze mozmy miec z nim problem a chcialbym
wiedziec jak takie przyklady rozwalac
11 paź 18:00
Aga1.:
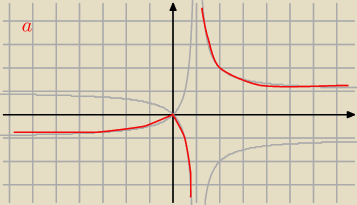
11 paź 18:18
Aga1.: W b) rozpatruj trzy przedziały , x≠0
11 paź 18:20
minikóper: aa czyli tak jak myslalem, dzieki
11 paź 18:40
