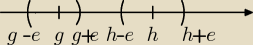dowód nie wprost
zakładamy, że istnieje taki ciąg który ma dwie granice: h,g
zadanie polega na tym, aby tak dobrać 'e' (e to jest ε>0 ) by te przedziały (g−ε,g+ε) i
(h−ε,h+ε) były rozłączne.Bo z definicji granicy ciągu prawie wszystkie wyrazy tego ciągu muszą
należeć do tego przedziału, więc jak będą należeć do jednego to do drugiego nie stąd ciąg ma
jedną granicę.
