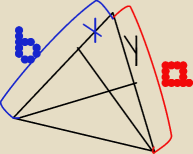
Podział podstaw w trojąkącie po zrzutowaniu wysokości kamila: Czy da się udowodnić, że bx = ay? dla dowlnego trójkąta ostrokątnego? y i x powstają po zrzutowaniu wysokości odpowiednio na boki a i b trójkąta.

Bogdan:

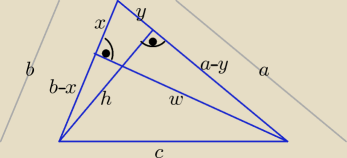
	⎧	x2 + w2 = a2
	⎩	y2 + h2 = b2

x² − y² + w² − h² = a² − b² ⇒ w² − h² = a² − b² − x² + y²

	⎧	w2 + (b−x)2 = c2
	⎩	h2 + (a−y)2 = c2

w² − h² + (b−x)² − (a−y)² = 0 ⇒ w² − h² = (a−y)² − (b−x)² a² − b² − x² + y² = (a−y)² − (b−x)² a² − b² − x² + y² = a² − 2ay + y² − b² + 2bx − x² 0 = −2ay + 2bx /:2 ⇒ ay = bx co należało udowodnić

kamila: Super, WIELKIE dzięki.

Bogdan: