Fizyka - ruch jednostajnie przyspieszony jok:

	m
Z powierzchni ziemi rzucono ciało do góry z prędkością początkową V0 = 5		, równocześnie
	s

	m
z wysokości hmax puszczono ciało z Vo = 5		. Oblicz czas i miejsce spotkania tych
	s

ciał. Prosze o wyprowadzenie wzorów:

	at12
h1max = V0t −		<< ruch opóźniony;
	2

Jak to policzyć dalej? Jak tutaj rozpocząć? Proponuję: 0 = v_o − at₁ < −− droga

	vo
t1 =
	a

	at12		V02		vo   a*( )2   a		V02
h1max = Vo * t −		=		−		=		−
	2		a		2		a

	v02
		= ....
	2a

Proszę sprawdzić

jok: dla v₂ zrobię to samo tylko zamienie na ruch przyspieszony, chodzi mi o rozpoczęcie zadania

jok: siup

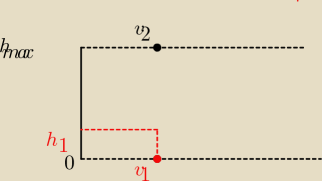
Nienor: Położenie ciała puszczone z góry opisuje równanie:

	gt2
h2(t)=vot+
	2

Położenie ciała z podrzuconego z dołu opisuje równanie:

	gt2
h1(t)=vot−
	2

Dla t=t_s się spotkają, czyli:

	gts2
h2=vots+
	2

	gts2
h1=vots−
	2

h_1max=h_2max, czyli w czasie t=t_s połorzenie ciała 1 zmieni się o

	gts2		gts2
Δh=h2−h1=vots+		−(vots−		)=gts2
	2		2

	gts2
gts2=vots−
	2

3gt_s²−2v_o=0

	2vo
3gts(ts−		)=0
	3g

	2vo
ts=
	3g

	1		10
Po podstawieniu ts=		[s] i wtedy już łatwo obliczyć h1=		[m].
	3		9

Chyba tak to ma być, bo z twojego to ci na pewno mogę powiedzieć, że ani droga, ani położenie nie są równe: 0=v_o−at. Nawet szybkość nie jest tyle równa w punkcie zderzenia, bo ciało nie uderzyło jeszcze w ziemię (wzleciało na maksmalną wysokość) więc jego v≠0, czyli ten wzór na szybkość ma postać v=v_o+at, dla danego t.