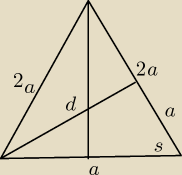
zadanie z planimetrii rg: Witam, Mamy zadanie: amię trójkąta równoramiennego jest dwa razy dłuższe od podstawy. Wyznacz obwód trójkąta, jeśli środkowa poprowadzona do ramienia ma długość d . I powiedźcie mi co robię źle.

	a   2
Na początku policzmy cos kąta s. cos s =		= 2
	a

Teraz z twierdzenia cosinusów:

	1		1
d2 =		a2 + a2 − 2 *		a *a * cos s.
	4		2

I tu już musi być gdzieś błąd bo dalej licząc nie wychodzi poprawna odpowiedź . Co jest nie tak?

Godzio: Środkowa nie pada na bok pod ktem prostym )

rg: a gdzie postąpiłem tak, jakbym wykorzystywał ten fakt? Bo jeśli chodzi o liczenie cosinusa, to liczę "z połówki trójkąta równoramiennego". No chyba, że twierdzenie cosinusów dt. tylko trójkątów prostokątnych, ale to byłby dla mnie szok, bo w szkole robimy dla każdego trójkąta ( chociaż z drugiej strony w mojej szkole niczemu nie należy się dziwić

Godzio: A dobra, źle popatrzyłem na rysunek Obliczenia są ok, może gdzieś coś źle liczysz ?

ZKS: cos(s) = 2 Jaki zbiór wartości ma funkcja y = cos(x)?

Godzio:

	a   2		1
cos(s) =		=
	2a		4

ZKS: I jak Godzio napisał zapewne tutaj jest błąd.

rg: faktycznie, jak mogłem tego nie zauważyć . Sam nie wiem co jest źle. wyszło, że d = a. A to nie jest przecież możliwe.