y=(x+6)^{32}-6 Rodney: Jak obliczyć miejsce zerowe funkcji z potega 32 ? Konkretnie chodzi o y=(x+6)³²−6 Jak wyznaczyć miejsce zerowe?

Artur_z_miasta_Neptuna: a skąd taka funkcja

Rodney: http://www.wat.edu.pl/N000000/images/stories/Archimedes_2011/Pliki/Fina_2011_tematy.pdf Zadanie 2

Eta: x+6 = p32{6} lub x+6= −p32{6} x= ..... lub x=.......

Rodney: x = p32{6} −6 lub x = −p32{6} −6 czyli nie da sie tego zrobic tak zeby mialo jakas ladniejsza postac? zaskoczylo mnie w ogole rozwiazanie myslalem, ze dojde do jakiejs ladnej liczby, tym bardziej, ze w zadaniu 1 otrzymalem wynik 72cm²

Artur_z_miasta_Neptuna: (x+6)³² − 6 = ((x+6)¹⁶)² − (√6)² = ((x+6)¹6 − √6)*((x+6)¹6 + √6) = = ((x+6)¹6 + √6)(((x+6)⁸)² − √6) = = ((x+6)¹6 + √6)((x+6)⁸ + ⁴√6)((x+6)⁸ − ⁴√6) = = ((x+6)¹6 + √6)((x+6)⁸ + ⁴√6)((x+6)⁴ + ⁸√6)((x+6)⁴ − ⁸√6) = =((x+6)¹6+√6)((x+6)⁸+⁴√6)((x+6)⁴+⁸√6)((x+6)²+6^1/16)((x+6)²−6^1/16)= =((x+6)¹6+√6)((x+6)⁸+⁴√6)((x+6)⁴+⁸√6)((x+6)²+6^1/16)(x+6+6^1/32)(x+6−6^1/32) dwa ostatnie nawiasy to pierwiastki rzeczywiste ... cała reszta to zespolone

Rodney: Arturze z miasta Neptuna podziwiam skilla i ogromne checi do rozpisania tego, ale nie mialem jeszcze liczb zespolonych, niewiele mi to daje liczylem po prostu, ze jest jakis sposob na sprowadzenie tego do ladniejszej postaci i ze chwilowe zacmienie w mozgu nie pozwala mi tego sposobu dojrzec w kazdym razie dziekuje za wlozony trud i checi

Artur_z_miasta_Neptuna: Rodney −−− nie chcę nic mówić ... ale tak rozpisywaliśmy w liceum tylko ja zawsze się wkurzałem i 'odrzucałem' części z pierwiastkami urojonymi

ZKS: W tym zadaniu trudność polegała na znalezieniu ostatecznego wzoru (x + 6)³² − 6 a obliczyć pierwiastki to już z górki Eta napisała odpowiedź od razu. Ale zadanie ciekawe.

Rodney: no bardzo ciekawe, troche trwalo, znalezienie tego ostatecznego wzoru, najpierw kombinowalem z postacia iloczynowa, bo myslalem, ze wtedy moze jakos ladnie beda pokazane miejsca zerowe, ale pokazalem zadanie mojemu matematykowi i powiedzial, ze trzeba zrobic to z postaci kanonicznej bardzo cwane, a skoro juz podalem linka, to moze ktos powie jak zabrac sie za zadanie 3? gdzie szukac pomocy do tego? jest jakis dzial na matematyka.pisz.pl gdzie znalazlbym potrzebna wiedze teoretyczna do tego?

ZKS: Właśnie trzeba było zauważyć że jeżeli napiszemy postać kanoniczną to ta 6 będzie ciągle redukowana. Jak geometria to ja nie pomogę.

Artur_z_miasta_Neptuna: to 3 zadanie trochę pod topologię można by było podciągnąć. zajmimy się tylko zbiorem A: 1^o ...odmierz odcinek długości '4' przechodzącą przez punkt 'O'

Artur_z_miasta_Neptuna: 2^o zauważ, że jeżeli 'S' nie leży na prostej przechodzącej przez P i O to odległość jest liczona jako odcinek PO + OS w takim razie odcinek PO jest 'stały' w punkcie1^o wyznaczyłeś 'długość' odcinka OS −−− wystarczy że zatoczysz 'koło' wokół punktu O o promieniu 'długości' odcinka OS i już masz zaznaczone wszystkie możliwe płożenia punktu S ... tak by dist (P,S) = 4

Artur_z_miasta_Neptuna: tak więc ... wynikiem będzie koło o środku O i promieniu = 4−|PO| = 1

Artur_z_miasta_Neptuna: jedyne z czym można spekulować ... to czy punkt (1;0) także będzie zawarty ... czy będzie bez tego (jednego) punktu. wynika to z zapisu, że: dist (M,N) = |MN| , gdy punkt O należy do prostej MN (jeżeli jest odcinek ... to punkt (1;0) należy ... jeżeli chodzi o prostą przechodzącą przez MN to wtedy nie należy ... bo dla tego przypadku, O należy do prostej więc dist(PS) = 2, a nie 4)

Rodney: o... dziekuje bardzo sprobuje to na wolno przeanalizowac i zrozumiec

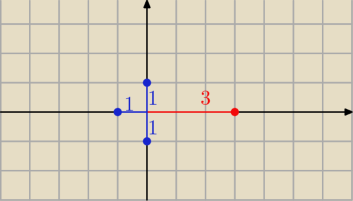
Artur_z_miasta_Neptuna: przyjmując ... że w tym zapisie : gdy punkt O należy do prostej MN traktujemy, że ów prosta jest to prosta przechodząca przez punkty MN (oba mogą być położone po tej samej stronie osi OY) to rozwiązaniem będzie

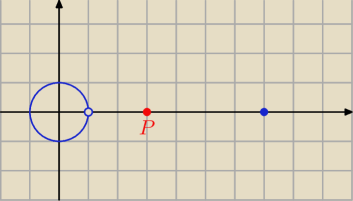
Artur_z_miasta_Neptuna: wyglądał tak (zauważ, że nie ma punkt (1,0) ale jest punkt (7,0) )

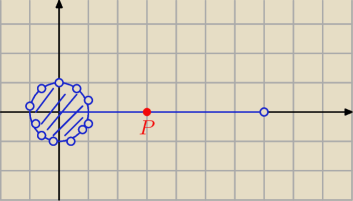
Artur_z_miasta_Neptuna: B to koło o środku w (0,0) i promieniu 1 BEZ obrzeża ∪ odcinek (−1;0) − (7;0) bez krańców odcinka (czyli punkt (1;0) NALEŻY do rozwiązania −−− co się zgadza bo odległość (3;0) do (1;0) wynosi 2)