wyznacz a ∪b ,a ∩b a/b b/a gdy A<1,4> B<2,5> Domcio: wyznacz a ∪b ,a ∩b a/b b/a gdy A<1,4> B<2,5>

ewa: A∪B=<1,5> A∩B=<2,4>

ewa: A\B=<1,2) B\A=(4,5>

Krzysiek : Przeciez mozesz narysowac sobie te przedzialy beda z kropkami zamalowanymi bo sa domkniete i wyznaczyc sume roznice i iloczyn zbioru a nie czekac na gotowe .

Bogdan: Nie potrzeba zamalowywać kropek. A∪B = <1, 5) A∩B = <2, 4> A \ B = <1, 2) B \ A = (4, 5) Uwaga: różnicę zbiorów oznaczamy A \ B, a nie A / B (stosujemy znak \, a nie znak /), ponadto zazwyczaj zbiory oznacza się dużymi literami, a ich elementy małymi literami.

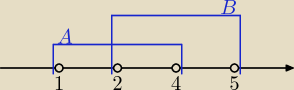
Bogdan: Jeśli A = <1, 4>, B = <4, 5>, to: A∪B = <1, 5> A∩B = <2, 4> A \ B = <1, 2) B \ A = (4, 5>

Krzysiek : Bogdan. W szkole tak ucza o tych kropkach i niech tak zostanie .

Gustlik: 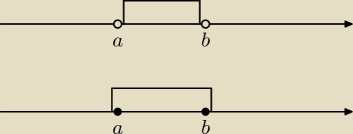Krzysiek, Bogdan ma racię, ale niestety nasi nauczyciele są niereformowalni i przyczepiają się do tych kropek, dlatego ja proponuję sposób "mieszany" Bogdana ze szkolnym. Zdarza się, że nauczycielka nie uzna tak zrobionego zadania, miałem taki przypadek niestety. Pierwszy rysunek to przedział (a, b), a drugi to <a, b>. Ja uczę tym "mieszanym" sposobem, uczeń wówczas tak samo widzi, co dzieje się na koncach przedziału, jak w metodzie Bogdana, a jest pewność, że nauczycielka się nie przyczepi. Niemniej metodę Bogdana uważam za rewelacyjną, robiąc nawet sposobem mieszanym udało mi się wyeliminować u uczniów błędy z odczytywaniem końców przedziału zwłaszcza w działaniach typu A\B czy B\A, bo uczeń widzi, czy kropka leży wewnątrz czy na zewnątrz przedziału.

aniab: a taki sposób jeszcze się używa? <a,b)

Krzysiek : Gustlik. Alez ja nawet nie probuje kwwestionowac tego co pisze BOgdan. MI sie tez to podoba i nawet ja to rozumiem To bedzie tak samo jak ucza przy wartosciach bezwzglednych IxI =x dla x≥o i −x dla x<0 a dlaczego nie zapisac tak IxI =x dla x>0 i −x dla x≤o . Przeciez tez tak mozna . No ale tyle lat ucza tym sposobem ze tak jak piszesz ze sa niereformowalni .pozdrawiam

aniab: bo to bardziej intuicyjne, że zero bez znaku jest razem z plusem którego też zazwyczaj się nie dopisuje przed dodatnimi ;>