objętość tomek : Witam mam prośbe musze obliczyc objętośc bryły ograniczonej powierzchniami x²+y²=4 , z=√x²+y² , z= z²+y²+6 wiem że tefigury to walec, paraboloida i stożek tylko nie wiem jak to będzie wyglądało, może mi ktos to narysować tak mniej więcej? bardzo prosze

Godzio: z = x² + y² − 4 Rysujesz x² − 4 i obkręcasz z = √x² + y² Rysujesz √x² = |x| i obkręcasz (to narysowałem)

tomek : kurcze ja tutaj widze dwa stożki odwrócone nic poza, a wydaje mi sie że miała byc tam paraboloida i walec chyba, możesz mi to jakoś innaczej narysowac lub opisać bo nie bardzo rozumiem o co w tym chodzi

Godzio: z = x² + y² − 4 Paraboloida

tomek : o matko, teraz mam kaszanke w głowie a wyrażenie z= z²+y²+6 to nie jest paraboloida przesunieta na osi z o 6 jednostek w góre

Godzio: Chyba jest, ale to "kopnięta" bo będzie raczej w płaszczyźnie ZOY

tomek : czyli przepraszam ale cięzko mi to idzie, wręcz opornie

tomek : Bardzo prosze o pomoc

Godzio: Czyli to samo, tylko osie nazwij inaczej

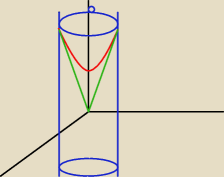
tomek : przecierz tam powinien być walec o promieniu r=2 paraboloida przesunieta o 6 jednostek po z i stożek w pkt (0,0,0)

tomek : na czerwono jest paraboloida zaczynajaca sie w pkt 6 stozek zaczyna sie w pkt (0,0,0) i pozostaje walej o promieniu 2

tomek : mam racje czy nie

Godzio: Masz

Godzio: Ale to będą krzywe w różnych płaszczyznach, a nie wszystkie tak jak Ty narysowałeś

tomek : To dobrze ze sie zgadzamy teraz jak zapisać tutaj całeczke do liczenia tej objetości wiesz może

tomek : nie wszystkie będą po osi Z przecierz, walec jest po Z stożek też i paraboloida też

Godzio: Całeczki Ci nie powiem, bo jeszcze nie miałem całek podwójnych/potrójnych

tomek : a kto może wie

Krzysiek: zrzutujmy to wszystko na płaszczyznę OXY, otrzymamy okrąg x² +y² =4 przejdźmy na współrzędne biegunowe: x=rcosδ y=rsinδ |J|=r z równania okręgu wynika,że: r∊[0,2] oczywiście δ∊[0,2π] płaszczyzna od góry ograniczająca bryłę to: z=x² +y² +6 (paraboloida) czyli: z=r² +6 od dołu stożek: z=√r² zatem objętość bryły to: ∫₀^2π (∫₀² (r² +6−r)|J| dr )dδ