Ostrosłup prawidłowy czworokątny . . . V.Abel: Dany jest ostrosłup prawidłowy czworokątny o podstawie ABCD i wierzchołku P. Długość krawędzi bocznej i krawędzi postawy jest jednakowa i wynosi a. Z wierzchołka C poprowadzono odcinek do środka krawędzi AP w punkcie S. Oblicz cosinusy kątów ΔACP: a) z użyciem Tw.Cosinusów b) bez jego użycia. Proszę o pomoc : a) gdy liczę tylko z Tw. Cos, to mi wychodzi, ale gdy najpierw z Tw. Sinusów wyznaczam sin, a potem z jedynki trygonometrycznej to mam 2 cosinusy i który mam wybrać? b) jak się za to zabrać?

V.Abel: hej, pomozecie ?

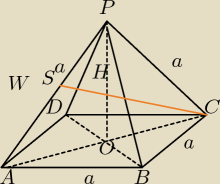
Mila: ΔACP:trójkąt jest równoramienny AC=a√2 (przekątna kwadratu o boku a) |AC|²=a²+a²−2a²cos∡APC (a√2)²=2a²−2a²cos∡APC cos∡APC=0 ⇔∡APC=90⁰ ∡PAC=∡ACP=45⁰

	√2
cos450=		co wyjdzie z tw, cosinusów
	2

a²=(a√2)²+a²−2a√2*acos∡ACP

	1		√2
cos∡ACP=		=
	√2		2

II sposób WΔPOC:

	0,5a√2
cos∡PCO=
	a

	√2
cos∡PCO=
	2

H²=a²−(0,5a√2)² H=0,5a√2=OC trójkąt równoramienny

	√2
cosOPC=		}
	2

dalej chyba wiadomo Tylko nie wiem, czy dobrze napisałeś trójkąt w którym trzeba obliczyc te cosinusy.

V.Abel: Dzięki , faktycznie ten trójkąt, to ASP Wyszły mi takie cos: −{5}/5 3√10/10 √2/2 czy tak ? .

Mila: Policzę.

Mila: Abel napisz dobrze ,który Δ. Nie ma ΔASP.

V.Abel: ΔACS, przepraszam, wpisując tu zadanie, zmieniłem oznaczenia, są odwrotnie, niż w treści, którą mam na kartce. Dzięki

Mila: W ΔACS:

	−√5
cos∡S=
	5

	√2
cos∡A=
	2

	3√10
cos∡C=
	10

V.Abel: czyli tak samo Dzięki ogromne ! ! ! Mogłabyś podpowiedzieć jeszcze w jednej rzeczy? Mam czworościan foremny. Przez krawędź podstawy oraz połowę przeciwległej krawędzi poprowadzono płaszczyznę. Oblicz cosinus kąta tej płaszczyzny do płaszczyzny podstawy. Czy to jest ten sam kąt, co kąt wysokości boku do podstawy?

V.Abel: no i mi wychodzi cos √3/2, czyli 60 stopni, a odp jest √6/3

Mila:

	a√3
h=
	2

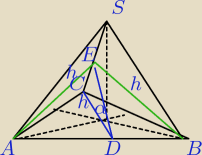
	√2
|ED|=		z tw Pitagorasa w ΔEDB
	2

	1		a√3		√2		a√3		√2
(		a)2=(		)2+(		)2−2*		*		cosα
	2		2		2		2		2

po przekształceniach

	√6
cosα=
	3

V.Abel: Ok, dzięki. Też mi wyszło .. w końcu ! ! ! Mi się na początku wydawało, że kąt CBS jest tym szukanym kątem, jednak nie. Dziękuję

Mila: To, dobrze, że w końcu zrobiłeś.