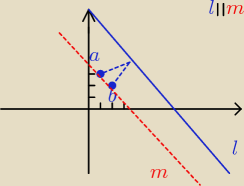
aż 7 pkt ! radek: chodzi mi o male wyjasnienie Na prostej l: x+y−6=0 wyznacz taki punkt C, aby dlugosc łamanej ACB, gdzie A(1,3) , B(2,2) byla najmniejsza. Uzasadnij swoje rozumowanie no wlasnie jak to uzasadnic bo niby sprawa jest prosta− widac ze prosta przechadzaca przez AB jest rownolegla do prostej l i czy uzasadnieniem moze byc ze ze ta lamana jest najkrotsza gdy |AC| = |BC| bo te proste sa rownolegle?

Bogdan: Przerzuć jeden z punktów na drugą stronę prostej l, np. punkt B, otrzymasz punkt B', połącz ten punkt B' z punktem A. Zobaczysz na prostej l właściwe położenie punktu C.

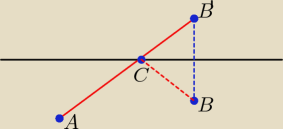
Bogdan: |B'C| = |BC|

radek: pamietam kiedys ktos mi podobnie tlumaczyl, Bogdan nie musze jakiegos komentarza dac do uzasadnienia? czy wystarczy samo przeksztalcenie i obliczenia?

Bogdan: Przydałby się mały komentarz, np. taki: najmniejsza odległość między 2 punktami jest równa długości odcinka łączącego te punkty i leżącego na prostej zawierającej te punkty. Tutaj tym odcinkiem jest AB'.

radek: dzieki Bogdan calkiem zgrabnie powiedziane