Liczby zespolone
jok:
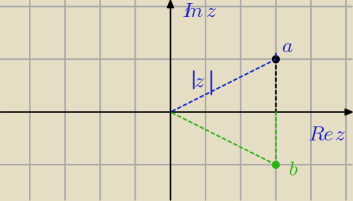
Witam, jak policzyć argument liczby zespolonej?
arg φ = 2π − α
0
−z = −x − yi
przykład
a)
z = 3 + i << punkt leży na I ćwiartce
|z| =
√9+1 =
√10
b)
z= 3 − i << leży na IV ćwiartce
To co wiem
Jak obliczyć argument główny?
9 paź 23:15
Vizer: Arcusami jedziesz

9 paź 23:20
Mila: Albo przybliżone wartości z tablic, w zależności od potrzeb.
9 paź 23:22
Basia:
ad.1
odczytać z tablic i zamienić na radiany
ad.2
2π − to co wyszło w (1)
albo napisać
| | | | 1 | |
(1) α0 = arctg |
| = arctg |
| |
| | | | 3 | |
| | | | 1 | |
(2) α0 = arctg |
| = arctg(− |
| ) |
| | | | 3 | |
9 paź 23:22
9 paź 23:24
jok: skąd to się bierze? nie mam takiej wiedzy

| | 1 | |
Skąd mam wiedzieć ile to jest arctg |
| ? |
| | 3 | |
9 paź 23:30
Vizer: Witam
Basię i
Milę, wreszcie dorwałem neta

9 paź 23:30
Vizer: Arcusy to funkcje odwrotne do funkcji trygonometrycznych, czyli tak zwane funkcje
cyklometryczne, jeśli nie miałeś jeszcze, to chwila google hackingu i się dowiesz

A co do
| | 1 | |
wartości arctg |
| to tak się zostawia jako wartość dokładną. |
| | 3 | |
9 paź 23:33
Mila: Witam Vizer.

Te funkcje cyklometryczne są w Skoczylasie.
9 paź 23:47
jok: dupa blada nie rozumiem tego, dzisiaj na zajęciach wszystko zrozumiałem nawet tw. de Moivre(czy
jakos tak) ale te argumenty ciągle mnie dręczyły.
może ktoś pokazać krok po kroku jak to się liczy?
np.
sinφ {−1}{
√2}
9 paź 23:53
jok: dzięki Mila, zaraz spojrzę

9 paź 23:54
Mila: Jok, na ogół są takie argumenty, że kąty w miarę łatwo się wyznacza.
Podaj liczbę zespoloną , to Ci wyznaczę.
9 paź 23:57
jok: a) 1−i
b) −2 −i
Tylko powoli

9 paź 23:59
jok: przepraszam, chciałeś łatwe argumenty b jest złe
niech
b) −√3 −1
10 paź 00:04
Mila:
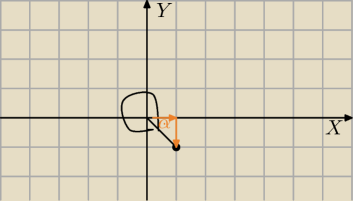
a)z=1−i to mam punkt (1;−1)
|z|=
√2
| | 1 | | √2 | |
Φ=3150 możesz policzyć z Δ cosα= |
| = |
| ⇒α=45 |
| | √2 | | 2 | |
Φ=(360−45)=315
0
To jest taki sposób na chłopski rozum.
Lokalizujesz Φ, liczysz sin albo cos dla kąta ostrego i obliczasz wartość Φ.
10 paź 00:26
jok: b) −
√3 +1
z= 2
Co teraz,które wybrać?
10 paź 00:33
Basia:
jest jeden i tylko jeden kąt z przedziału <0;2π) spełniający te warunki
sinus>0 i cosinus<0 ⇒ II ćwiartka
czyli α=π−
π6 =
5π6
10 paź 00:36
jok: φ = 180−α
| | 1 | | 5 | |
argument = π − |
| = |
| π |
| | 6 | | 6 | |
dobrze rozumiem?
10 paź 00:36
Mila:
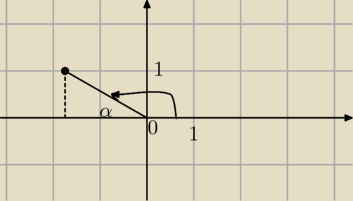
z=−
√3+i punkt(−
√3,1)
|z|=
√3+1=2
α=30
0
Φ=180−30=150
0
10 paź 00:40
Basia: dobrze

tylko litery w zapisie gubisz
a że to II ćwiartka to
α=π−
π6 =
56π=
5π6
10 paź 00:40
jok: dziękuje za pomoc

jutro mechanika , repetytorium z fizyki. Najbardziej lubię matematykę,
której wcale nie znam ale przyjemnego mam wykładowce i "ćwiczeniowca" który zachęca do
myślenia.
10 paź 00:45
Vizer: A najlepiej to się nie bawić z sinusami i cosinusami tylko tangensa policzyć, patrząc na
rysunek.
10 paź 00:46
 Witam, jak policzyć argument liczby zespolonej?
arg φ = 2π − α0
Witam, jak policzyć argument liczby zespolonej?
arg φ = 2π − α0



 A co do
A co do
 Te funkcje cyklometryczne są w Skoczylasie.
Te funkcje cyklometryczne są w Skoczylasie.


 a)z=1−i to mam punkt (1;−1)
|z|=√2
a)z=1−i to mam punkt (1;−1)
|z|=√2
 z=−√3+i punkt(−√3,1)
|z|=√3+1=2
z=−√3+i punkt(−√3,1)
|z|=√3+1=2
 tylko litery w zapisie gubisz
tylko litery w zapisie gubisz
 jutro mechanika , repetytorium z fizyki. Najbardziej lubię matematykę,
której wcale nie znam ale przyjemnego mam wykładowce i "ćwiczeniowca" który zachęca do
myślenia.
jutro mechanika , repetytorium z fizyki. Najbardziej lubię matematykę,
której wcale nie znam ale przyjemnego mam wykładowce i "ćwiczeniowca" który zachęca do
myślenia.