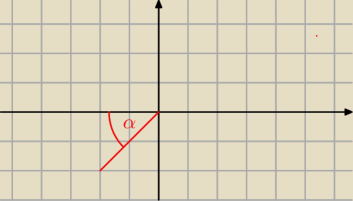
. asdf: sinφ = π + α albo sinφ = 3π − (π − α) czym jest dokładne te φ? i czym się różni od małego (fi) = Φ

asdf: 4 + 3i = (4,3) tak?

Krzysiek: a czego Ty szukasz konkretnie? argumentu liczby zespolonej? jeżeli tak, to wtedy φ=π+α pytasz się czym jest φ a tak naprawdę nigdzie tego nie użyłeś (na rysunku tego nie ma )

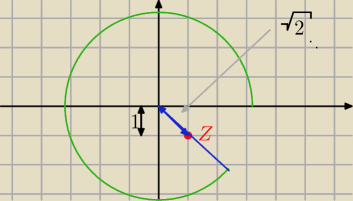asdf: Argument liczby zespolonej...czyli? jak mam takie coś: z = 1 − 2i, A = (1, −2) |z| = √1 + 4 = √5 Definicja: Argumentem liczby zespolonej z = a + bi nazywamy liczbę Φ spełniającą równania: 0≤φ(argument główny)≤2π Φ = φ + 2kπ Miara łukowa = Φ

	a
cosΦ =		−−−> a = |z|*cosΦ
	|z|

	b
sinΦ =		−−−−−> b = |z|*sinΦ
	|z|

z = a + bi = |z|cosΦ + i*|z|*sinΦ = |z|(cosΦ + isinΦ) i teraz mam takie coś, co w ogóle nie rozumiem: postać trygonometryczna

	7π		7π
z = 1 − i = (1, −1) = √2 * (cos		+ i * sin		)
	4		4

	1		π		7π
cosφ =		−−−−> cosφ = 2π −		=		<<< z kąd taki zapis?
	√2		4		4

	−1
sinφ =
	√2

ODNOSZĄC SIĘ DO RYSUNKU:

	1		7π
cosφ		<−−−−to rozumiem, ale z kąd się wzięło
	√2		4

|z| = długość punktu z od punktu (0,0)

asdf: dokładnie nei wiem czym jest ten ∡φ oraz ∡Φ Można mi to jakoś wytłumaczyć

Godzio: z = 1 − i

	1
cosφ =
	√2

	1
sinφ = −
	√2

W której ćwiartce jest cosinus dodatni, a sinus ujemny ? Ano w IV, więc kąt φ musi być w czwartej ćwiartce

	π		1
cos(		) =		− musimy pójść do IV ćwiarki, czyli:
	4		√2

	π		7
cos(2π −		) = cos		π
	4		4

asdf: a już samo to, że punkt z = 1 − i znajduje się w 4 ćwiartce nie "uświadamia", że te kąty są w 4 ćwiartce? czym jest dokładnie ten kąt ∡φ oraz czym się różni od∡Φ

asdf: i jeszcze mam pytanie: jak wygląda postać kartezjąńska liczby zespolonej? tak: (a,b) = a + bi?

Godzio: Ten sposób co podałem to taki bezmyślny Widać to po rysunku, że w 4 Argument główny (oznaczamy arg(z) ) to kąt między tym wektorkiem (tym "promieniem" co narysowałeś) a osią rzeczywistą (licząc przeciwnie do wskazówek zegara)

Godzio: Tak

Godzio: A kąt Φ to jak już troszkę teorii będziesz miał, bo to trochę więcej roboty (nie trudne ) Jak będziemy liczyć np pierwiatki takiej liczby:

	φ
6√√3 + i wtedy naszym kątem będzie: Φ =		, w zależności od ilości pierwiastków
	6

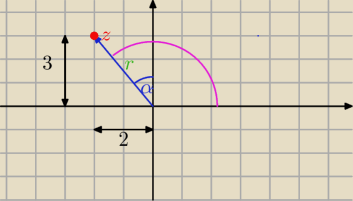asdf: ok, czyli jak mam taki punkt: z = −2 + 3i = (−2,3) |z| = √4 + 9 = √13 można przyjąć, że |z| = r? czyli sinφ = sinφ(90 + α) = przechodzi w cofunkcje, znak dodatni (II ćwiartka) =

	3
= +cos(α) =
	√13

tak?

asdf:

asdf: ?

Krzysiek: tak, dorysuj sobie trójkąt prostokątny (o przeciwprostokątnej 'r' ) a wtedy od razy widać,że:

	2
sinα=
	r

	3
cosα=
	r

r=|z|

asdf: Ok . Dzięki