Dla jakiej wartosci parametru, dla jakiego a d4mian: 1) Dla jakich wartości parametru |2x−1|=m parabola ma a) 0 rozwiązań b) 2 rozwiązania 2) Dla jakich a spełniona jest nierówność a³ > a⁵

Mila: Popraw treść (1) , nie widzę paraboli. 2) a³−a⁵>0⇔a³*(1−a²)>0⇔a³(1−x)(1+x)>0 dalej sam rozwiąż.

Mateusz: Miało byc chyba |2x²−1| narysuj te funkcje i rozwaz przypadki dla a) i b) kiedy to równanie ma rozwiązania 2) Zastanów się jakie muszą być podstawy a konkretnie zaleznosc między nimi

d4mian: A więc: 1) Dla jakich wartości parametru |2x²−1|=m parabola ma a) 0 rozwiązań b) 2 rozwiązania 1)Rysunek: http://m01i.img-up.net/rys75c4.jpg no to wg rysunku 2 rozw od <0,1)v(1,∞) 0 dla m <0 dobrze? 2) a³(1−x)(1+x)>0 a= 0 v x = 1 v x = −1 > 0 więc x = 1 ?

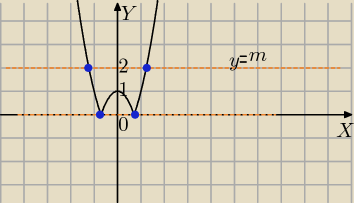
Mila: 1) a)dla m<0 zero rozwiązań b) Dla m=0 dwa rozwiązania (przecięcie wykresu w dwóch punktach) dla m>1 dwa rozwiązania ( dla m∊(0,1) 4 rozwiązania, dla m=1 są 3 rozwiązania) 2) napisz w jakich przedziałach

Aga1.: 1) rysunek dobrze, ale pierwszą część odpowiedzi trzeba poprawić Równanie ma 2 rozwiązania dla m∊{0}U(1,∞)

d4mian: 2) przedziały a∊ (1,∞)

d4mian: dobry przedział?

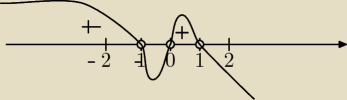
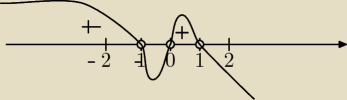Mila: a³(1−a)(1+a)>0⇔a∊(−∞;−1)∪(0;1) W poście 17:17 była litrówka ( było x zamiast a)