prawdopodobieńśtwo Caroline: Proszę o rozwiązanie tego ciekawego zadanka: W urnie znajduje się n kul białych i 2n kul czarnych. Losujemy dwie kule. Jakie musi być n, aby prawdopodobieństwo wylosowania pary kul tego samego koloru było równe prawdopodobieństwu wylosowania kul różnokolorowych?

Bogdan:

	3n 2		3n(3n − 1)
|Ω| =		=
			1 * 2

n 2

2n 0

n 0

2n 2

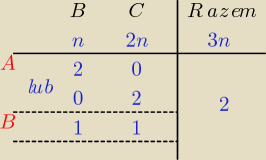
n(n − 1)

2n(2n − 1)

|A| =

*

+

*

=

* 1 + 1 *

1 * 2

1 * 2

	n 1		2n 1
|B| =		*		= n * 2n

	|A|		|B|
P(A) =		, P(B) =
	|Ω|		|Ω|

P(A) = P(B) ⇒ .... dokończ

pigor: ... widzę to tak :

n 2   2n 2   +		n 1   2n 1   *
	=		i n>2 ⇒
3n 2		3n 2

n 2

2n 2

n 1

2n 1

n(n−1)

2n(2n−1)

2

⇒

+

=

*

⇔

+

= n*2n /*

⇔

2

2

n

⇔ n−1+2(2n−1) = 2*2n ⇔ n−1+4n−2 = 4n ⇔ n=3 i to by było tyle . ...