 Witam,
proszę o pomoc z tym zadankiem
Witam,
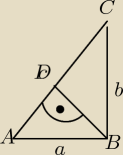
proszę o pomoc z tym zadankiem  W trójkącie rozwartokątnym ABC poprowadzono wysokość BD, która podzieliła ten trójkąt na dwa
trójkąty tak, że trójkąt ADB jest trójkątem równoramiennym. Oblicz promień R okręgu opisanego
na trójkącie ABC
b = 4(1+sqrt(3))
a= 4*sqrt(2)
W trójkącie rozwartokątnym ABC poprowadzono wysokość BD, która podzieliła ten trójkąt na dwa
trójkąty tak, że trójkąt ADB jest trójkątem równoramiennym. Oblicz promień R okręgu opisanego
na trójkącie ABC
b = 4(1+sqrt(3))
a= 4*sqrt(2)
 Nie umiesz napisać poprawnej treści zadania, a oczekujesz poprawnej odpowiedzi?
Poprawna treść zadania :
W trójkącie rozwartokątnym ABC o kącie rozwartym przy wierzchołku B
poprowadzono wysokość BD, która podzieliła ten trójkąt na dwa trójkąty tak,że trójkąt ADB
jest równoramienny.
Wiedząc,że długości boków: |AC|= 4(1+√3) i |AB|=4√2
Oblicz długość promienia R okręgu opisanego na trójkącie ABC.
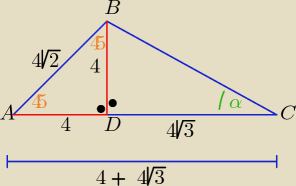
ΔADB jest prostokątny i równoramienny, to |AD|=|BD|= 4
|DC|= |AC|−AD|= 4+4√3−4= 4√3
Nie umiesz napisać poprawnej treści zadania, a oczekujesz poprawnej odpowiedzi?
Poprawna treść zadania :
W trójkącie rozwartokątnym ABC o kącie rozwartym przy wierzchołku B
poprowadzono wysokość BD, która podzieliła ten trójkąt na dwa trójkąty tak,że trójkąt ADB
jest równoramienny.
Wiedząc,że długości boków: |AC|= 4(1+√3) i |AB|=4√2
Oblicz długość promienia R okręgu opisanego na trójkącie ABC.
ΔADB jest prostokątny i równoramienny, to |AD|=|BD|= 4
|DC|= |AC|−AD|= 4+4√3−4= 4√3
| 4 | 1 | |||
tgα= | = | ⇒ α= 30o | ||
| 4√3 | √3 |
| |AB| | ||
z tw. sinusów | = 2R ⇒ R=.......... | |
| sinα |