trapez M.: w trapezie rownoramiennym o podstawach dlugosci a i b oraz kacie ostrym α=60 polaczona srodki sasiednich bokow oblicz pole czworokata ktorego bokami sa te odcinki

tim: Ja próbuję.

M.: o dzieki Ci tim...

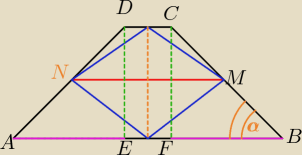
tim: Odcinki AB = a CD = b

	a + b
MN = m =
	2

Pole figury niebieskiej = pole rombu o przekątnych MN oraz CF. MN mamy, ale brakuje nam wysokości. Bierzemy trójkąt CFB i tak.

	a − b
Odcinki fioletowe (bo to jest tr. równoramienny) =
	2

	√3(a − b)
Z funkcji tryg. obliczamy h =
	2

	MN * h
Polerombu =
	2

	a + b   √3(a − b)   * 2   2
Polerombu =
	2

Teraz może zastosować wzór skróconego mnożenia i poskracać.

M.: ah... tak to ma wygladac dziekuje

tim: Tfu. Jakie poskracać. Nie poskracać tylko wymnożyć

M.: powiedz mi tylko jeszcze jedno... skad Ty masz taka glowe? da sie gdzies kupic ?

tim: Dostałem od mamusi dokładnie 15 lat i 1 dzień temu

M.: za odp hehe