Geometria Analityczna
Vercuz: Dane są okręgi o równaniach: (x − 3)2 + y2 = 9 i (x − 6)2 + y2 = 9.
a) Wyznacz miary kątów BS2A i BS1A, gdzie S1, S2 są środkami odpowiednio pierwszego i
drugiego okręgu, zaś A, B − wspólnymi punktami okręgów.
b) Wyznacz pole części wspólnej kół ograniczonych tymi okręgami.
c) Wyznacz współrzędne punktów A i B.
8 paź 18:30
Kin: Ja bym to zrobiła tak
a)
S1 = (3,0) r1 = 3
S2 = (6,0) r2=3
Tworzysz układ równań z tych równań okręgów. Rozwiązujesz go metodą podstawiania i wychodzą ci
dwa rozwiązania
| | 1 | | 3 | |
1) x= 4 |
| , y = √6,75 = |
| √3 |
| | 2 | | 2 | |
| | 1 | | 3 | |
2) x= 4 |
| , y = − √6,75 = − |
| √3 |
| | 2 | | 2 | |
Następnie szukasz wzoru prostej przechodzącej przez punkt S1 i A też układem równań i wychodzi
y =
√3x −3
√3
tg (β) = a
tg (β) =
√3
β = 60 stopni
∡ BS
1A = ∡ BS
2A = 2β = 120 stopni
8 paź 19:53
Kin:
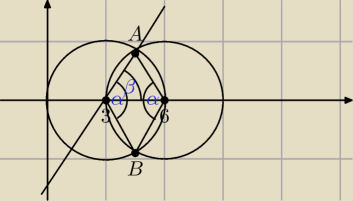
8 paź 20:02
Kin: B)
Obliczasz pole trójkąta S1 S2 A i pole wycinka 120 stopni
Pcz.wspólnej = 2*Pwycinka − 2*Ptrójkąta
8 paź 20:22
Vercuz: Dzięki, już na to wpadłem

8 paź 20:39

