trapez
max: Dany jest trapez ABCD o podstawach AB = 20 cm i CD=16 cm oraz bokach AD=8 cm i BC= 10 cm. Boki
nierównoległe przedłużono do przecięcia w punkcie P i na przedłużeniu DP odmierzono odcinek PM
= 10 cm. Z punktu M poprowadzono prostą l równoległą do AB przecinającą przedłużenie CP w
punkcie N. oblicz długości odcinków MN i PN
8 paź 13:45
max: Jak to zrobić pomoże ktoś?
8 paź 13:46
max: Wyjdzie nam tu trójkąt MNP i mamy dany jeden bok PM=10cm jak obliczyć te kolejne boki? Czy mam
tu obliczyć pole a potem skorzystać z twierdzenia Pitagorasa?
8 paź 13:59
aniab: z Talesa tylko
8 paź 14:02
aniab:
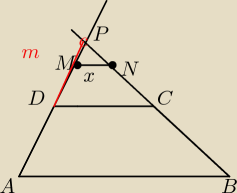
czerwona to m
potem
itd y
8 paź 14:07
aniab: y chyba 12,5
8 paź 14:08
max: w tym twierdzeniu maja wspólną podstawę a tu nie. jak to rozpocząć?
8 paź 14:15
max: dzięki
8 paź 14:15
Aga1.:
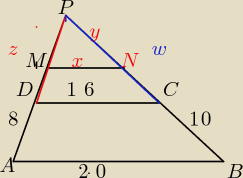
z=IDPI
IAPI=8+z
IDMI=z−10
INCI=w−y
IPNI=y , IPMI=10
8 paź 14:18
max: i co dalej? proszę
8 paź 14:23
max: czyli to teraz wyliczyć i podstawić prawda
8 paź 14:33
max: czyli x= 5 a y=12,5
8 paź 14:52
max: dzięki serdeczne

8 paź 14:53
max: mam jeszcze jedno zadanko
Ostrosłup prawidłowy sześciokątny ma wysokość h dwa razy większą od krawędzi podstawy. Oblicz
długość krawędzi bocznej oraz kąt α ściany bocznej przy wierzchołku ostrosłupa.
Jak to zrobić? Proszę o pomoc.
8 paź 14:59
Aga1.:
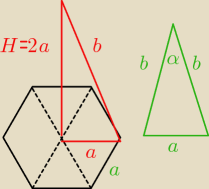
b=
√a2+4a2=a
√5
cosα wyliczysz z twierdzenia cosinusów
a
2=b
2+b
2−2b*bcosα
8 paź 16:03
macko: mogę prosić o więcej informacji? proszę
8 paź 16:17
Aga1.: b2=5a2
Podstaw do ostatniego wzoru za b2
i oblicz cosα,
8 paź 16:19
macko: a na co to są wzory?
8 paź 16:22
Aga1.: b wyliczyłam z twierdzenia Pitagorasa
b2=a2+H2
8 paź 16:26
macko: cosα = 9a2 / 2b
czy taki jest wynik
8 paź 16:26
Aga1.: | | 9a2 | | 9a2 | | 9 | |
cosα= |
| = |
| = |
| |
| | 2b2 | | 10a2 | | 10 | |
8 paź 17:59
macko: a skąd wzięłaś te 10a2 ?
8 paź 18:11
 czerwona to m
czerwona to m
 z=IDPI
z=IDPI

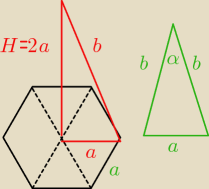 b=√a2+4a2=a√5
cosα wyliczysz z twierdzenia cosinusów
a2=b2+b2−2b*bcosα
b=√a2+4a2=a√5
cosα wyliczysz z twierdzenia cosinusów
a2=b2+b2−2b*bcosα