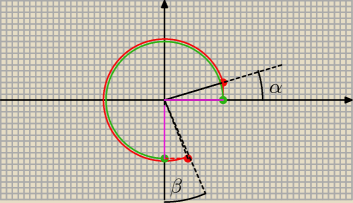
wzory redukcyjne jok: Witam, prosze o pomoc w wyznaczaniu prostych wzorow redukcyjnych GRAFICZNIE 90 + α, 90−α, 270+α. Później dodam następne z braku czasu. Pierwszy rysunek 270 + α = β c² = x² + b²

	y
sinα =
	c

	x
cosα =
	c

B(y,−x)

	y
sinβ =		= sinA
	c

	−x
cosβ =		= −cosA
	c

Ja to tak rozumuje, gdzie jest błąd i jak go poprawić, prosze o graficzny przykład.

Aga1.:

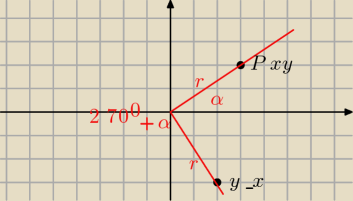
	y
sinα=
	r

	x
cosα=		, gdzie r=√x2+y2
	r

	−x
sin(2700+α)=		=−cosα
	r

	y
cos(2700+α)=		=sinα
	r

jok:

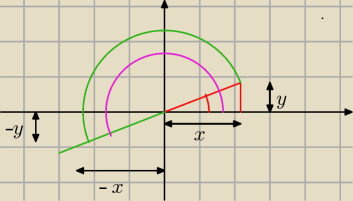
	y
sinx =
	r

	−y
sin(180 + x) =		= − sinx
	r

.

jok:

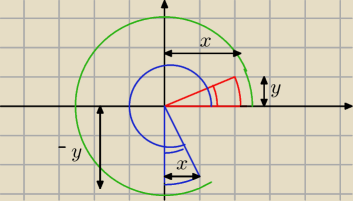
	y
sin(x) =
	r

	x
cos(x) =
	r

	x
sin(270 + x) =		= cosx
	r

	−y
cos(270 + x) =		= −sin(x)
	r

Aga1.: Rozwiązałam Ci ten przykład 0 12:31 Ale można bez wyprowadzania 270⁰+α to IV ćwiartka, w czwartej ćwiartce sinus jest ujemny i przechodzi w kofunkcję. sin(270⁰+α)=−cosα

Aga1.: A cos(270⁰+x)=sinx, bo cosinus dodatni w IV ćwiartce i przechodzi w kofunkcję.