Tw. cosinusów i o dwusiecznej. i-u: Dł. boków trójkąta wynoszą a,b i c. Znajdź długość odcinka dwusiecznej kąta naprzeciwko boku długości c, zawartego w tym trójkącie. Wiem, że trzeba to zrobić z twierdzenia o dwusiecznej i twierdzenia cosinusów, wiem, że dwusieczna dzieli bok c na odcinki cb/a+b i ca/a+b, ale za cholerę nie chce mi wyjść tak jak jest w odpowiedziach czyli √ab(a+b+c)(a+b−c)/a+b Bardzo proszę o pomoc, bo siedzę już nad tym naprawdę długo.

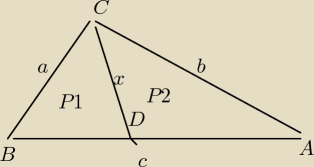
AS: Założenia: ∡ BCA = γ , ∡ BCD = ∡ DCA = γ / 2 , CD − dwusieczna kąta γ Tok obliczeń Kąt γ znajdujemy z tw. cosinusów cosγ = (a² + b² − c²)/(2*a*b) Pole całego trójkąta ABC PΔABC = 0.5*a*b*sinγ Pola P1 i P2 P1 = 0.5*a*x*sin(γ/2) , P2 = 0.5*b*x*sin(γ/2) P1 + P2 = PΔABC Podstawiam wyliczenia 0.5*a*x*sin(γ/2) + 0.5b*x*sin(γ/2) = 0.5*a*b*sinγ 0.5*x*sin(γ/2)*(a + b) = 0.5*a*b*sinγ 0.5*a*b*2*sin(γ/2)*cos(γ/2) x = −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 0.5*(a + b)*sin(γ/2) Po uproszczeniu a*b*cos(γ/2) x = −−−−−−−−−−−−−−−−−−−−−−− a + b

i-u: Dzięki wielkie!

ajdontnoł: co ma cosγ do cos(γ/2)? To rozwiązanie jest złe

Mila: II sposób Obliczam na jakie odcinki podzieliła dwusieczna bok c, z tw. o dwusiecznej kąta; e+f=c

	cb
e=
	a+b

	ac
f=
	a+b

Korzystam z twierdzenia: W każdym trójkącie iloczyn dwóch boków jest równy kwadratowi długości dwusiecznej kąta między nimi zawartego powiększonej o iloczyn odcinków , na które ta dwusieczna podzieliła trzeci bok]]. ab=d²+e*f

	cb		ca
d2=ab−		*
	a+b		a+b

	ab(a+b)2−abc2
d2=
	(a+b)2

	ab[(a+b)2−c2]
d2=
	(a+b)2

	ab(a+b−c)(a+b+c)
d2=
	(a+b)2

	√ab(a+b−c)(a+b+c)
d=
	a+b

Mila: http://www.wiw.pl/matematyka/geometria/geometria_10_04.asp Podaję Ci Link, gdzie jest dowód tego twierdzenia. Dowód twierdzenia.(310)

bnb: πΩ∊βαππππππππ