oblicz pole równoramiennego trójkąta prostokątnego aga: oblicz pole równoramiennego Δ prostokątnego, jeżeli jego przeciwprostokątna jest o 1+∫2 dłuższa od przyprostokątnej

Bogdan: chyba o 1 + √2

ZKS: Skoro jest to trójkąt prostokątny to wykorzystaj twierdzenie Pitagorasa. x² + x² = (x + 1 + √2)²

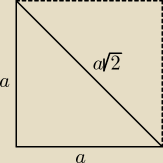
Bogdan: a√2 = a + 1 + √2 rozwiąż to równanie

aga: dzięki

Bogdan: Podaj aga swoje rozwiązanie

aga: wychodzą mi jakieś bzdury a w rozwiązaniu zadania jest wynik17/2+6√2 nie mam pojęcia skąd to się wzięło proszę pomóż

Bogdan: Pierwszy krok: a√2 − a = √2 + 1 Teraz Twój krok

aga: a√2−a=√2/√2

aga: zapomniałam jeszcze po prawej dopisać +1

Bogdan: To ja zrobię drugi krok a(√2 − 1) = √2 + 1 Teraz Twoja kolej

Eta:

aga: a(√2−1)=√2+1/:√2−1

	√2+1		√2+1
a=		*
	√2−1		√2+1

	5
a=
	3

czy to jest dobry wynik?