Pilne! AAAAAAAAAAAA: suma odległości na osi liczbowej liczby x od liczby 1 i −3 jest równa 5. wobec tego x spełnia równanie: A. |x − 1| +5 =|x+3| B.|x + 1| +5 =|x−3| C. |x − 1| +|x+3|=5 D. |x+1|+ |x−3 |=5

Eta: C)

AAAAAAAAAAAAAAAa: a skąd się to wzięło?

Eta: https://matematykaszkolna.pl/strona/1652.html

AAAAAAAAAAAA: ale mi pasuje dokładnie ten opisać

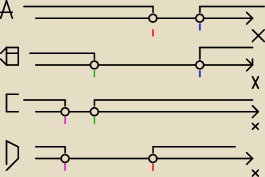
WWWWWW: kolor czerwony − cyfra 3 kolor niebieski − cyfra 9 kolor zielony cyfra − (−3) kolor rózowy cyfra− (−9) wskaż rysunek na którym jest przedstawiony zbiór rozwiązań nierówności |x+6| > 3 A B C D

WWWWWWWWW: ale mi o wyjaśnienie chodzi

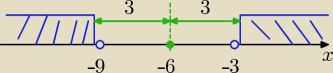
Eta: Tak powinien wyglądać rys; Na Twoim opisie, można dostać oczopląsu Odp: C)

WWWWWWWWWW: to w końcu odp C czy D?

Eta: C)

Eta: C)

WWWWWWWWW: ok, dziękuje

WWWWWWWWW: suma przedziałów (−∞;6) ∪ (6; +∞) jest zbiorem rozwiązań nierówności: A. |x|>6 B. |x|≥6 C. |x|<6 D. |x|≤6

Eta: A)

WWW: zbiór liczb których odległość na osi liczbowej od liczby 2 jest równa 4, można opisać równaniem: A.|x|=4 B.|x−2|=4 C.|x+2|=4 D. |x−2|=2

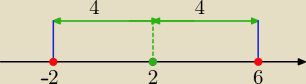
Eta: B) |x−2|=4 ⇒ x−2=4 v x−2= −4 x= 6 v x= −2

Eta: https://matematykaszkolna.pl/strona/1652.html Koniec pomagania w tego typu zadaniach Poczytaj w linku, który podaję !