dzielenie
Patison: (x+1):(x−1)=....
czy może mi ktoś pokazać sztukę dzielenia dwumian przez dwumian?
7 paź 18:31
7 paź 18:33
Patison: to nie ma końća to dzielenie:
| | 2 | | 1 | |
(x+1):(x−1)=1+ |
| + |
| i tak dalej bo ciągle reszta. |
| | x | | x2 | |
7 paź 18:44
sushi_gg6397228:
ma koniec, juz po pierwszym dzielenie
wychodzi reszta =2
7 paź 18:46
Eta:
x≠1
| x+1 | | x−1+2 | | x−1 | | 2 | | 2 | |
| = |
| = |
| + |
| = 1+ |
| |
| x−1 | | x−1 | | x−1 | | x−1 | | x−1 | |
7 paź 18:47
Mila: Może być tak:
| x+1 | | x−1+1+1 | | x−1 | | 2 | | 2 | |
| = |
| = |
| + |
| =1+ |
| |
| x−1 | | x−1 | | x−1 | | x−1 | | x−1 | |
albo
(x+1): (x−1)=1
−x+1
===
= 2 reszta
7 paź 18:51
Patison:
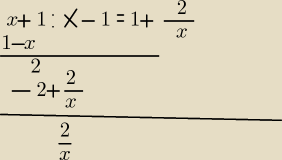
7 paź 18:56
Patison: Tą metodę znam ale przy trudniejszych liczbach jest kłopotliwa. Dobrze to?
7 paź 18:57
krystek: A jak zapisujesz 13:4=
7 paź 18:58
7 paź 19:00
krystek: I teraz popatrz na swój zapis 18:56
7 paź 19:01
Patison: nic mi to nie mówi

7 paź 19:05
krystek: To popatrz na zapisy Ety i sushiego
7 paź 19:06
Patison: to popatrz na mój: Tą metodę znam ale przy trudniejszych liczbach jest kłopotliwa.
Napisz jak albo przestać się drażnić.
7 paź 19:07
Patison: Dlaczego mila nie dzielisz tam dalej tej 2 tak jak ja? skąd wiadomo, ze to reszta?
7 paź 19:16
Gustlik: Tak jak wielomian przez wielomian:
1
−−−−−−−−−−−−−−−−−
−x+1
−−−−−−−−−
2
Ten sposób może służyć np. do przekształcenia wzoru funkcji homograficznej z postaci ogólnej na
kanoniczną i jest to najkrótszy i najłatwiejszy sposób przekształcania funkcji homograficznej.
| | 2 | | 2 | |
Np. f(x) |
| +1 → p=1, q=1, zatem wykres funkcji (hiperbolę) f(x)= |
| należy przesunąć |
| | x−1 | | x | |
o wektor w
→=[1, 1]
7 paź 22:37
Krzysiek : Patison. Zobacz . Podzieliles x+1:x−1 (zobacz tam na swoje dzielenie tam gdzieto obliczales ) .
Wyszlo CI ze to sie rowna 1 i pod kreska 2 Zgadza sie . tak.
Teraz sie zastanow . Chcesz dalej dzielic . Ile 2 miesci sie w x ze chcesz to dzielic . NIe
wiadomo ile . Wiec zostaje ta reszta 2 i nasze dzielenie bedzie wygladac tak
Inaczej by wygladala sprawa gdyby pod kreska wyszlo CI np 3x lub inne wyrazenie ale z x bo np
3x niesci sie 3 razy w x i wtedy mozesz dzielic dalej .
| | 1 | |
Jeszcze inaczej napisales Krystkowi z e 13;4=3 |
| . To teraz potraktuj ta 13 jako x+1 a 4 |
| | 4 | |
| | 1 | | 1 | |
jako x−1 i masz 3 |
| =3+ |
| ⇒jezeli 4 potratujesz jako x−1 to dla czesci ulamkowej tej |
| | 4 | | 4 | |
8 paź 12:14