rozwiązywanie nierówności z wartością bezwzględną maciek: zadania "prostackie" ale nie wiem czemu kilka wyników różni się od wersji wykonanej inną metodą. podam wynik z zajęć oraz mój:

	x
a) |x+1|≤		+2
	3

1) x+1≥0 2) x+1< 0 x≥−1 x< −1

	x		x
x+1≤		+2 /*3 −x−1≤		+2 /*3
	3		3

3x+3≤x+6 −3x−3≤x+6 2x≤3 −4x≤9

	3		9
x≤		x≥−
	2		4

	3		9
x∊<−1,		> x∊<−		,−1)
	2		4

	9		3		3
Moja odp: x∊<−		,		> odp z zajęć.: x∊<−6,		>
	4		2		2

b) |x|>x+1 1) x≥0 2) x<0 x>x+1 −x>x+1 0>1 (sprzeczne) −2x>1

	1
x<−
	2

	1		1
Odp moja x∊(−∞, −		) odp z zajęć: x∊<−1, −		)
	2		2

Proszę o sprawdzenie, czy rozwiązuję przykład w sposób prawidłowy lub ewentualnie gdzie się mylę. Pozdrawiam

sushi_gg6397228: bo bierzesz czesc wspolna rozwiania, a nie sumę

Eta: @maciek Twoja odp: do 1 zad. jest poprawna ! np dla x= −5 wykonaj sprawdzenie i okaże się....... ,że

Eta:

	1		1
zad2/ x< −		i x<0 to część wspólna : x€ (−∞, −		)
	2		2

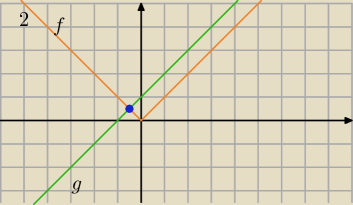Mila: f(x)=|x| g(x)=x+1 zielony

	−1
wykres f(x) leży nad wykresem g(x) dla x<
	2

[jeśli punkt jest niedokładny to liczymy tak: x+1=−x 2x=−1

	1
x= −
	2

	1
⇔|x|>x+1 dla x<−
	2

maciek: Dziękuje za szybką odpowiedź. jednak w dalszym ciągu nie wiem na czym stoję @ Eta i Mila : z waszych odpowiedzi wnioskuję , że moja odpowiedź do zadania 2. jest rówineż

	1
poprawna − x∊(−∞,−		). Przy wykonywaniu sprawdzenia wynika ( jeśli robie to jak
	2

	1
trzeba), że każda liczba x<−		spełnia równanie |x|>x+1
	2

To mi nie daje spokoju help me !

Mila: Mogły być na zajęciach jakieś inne nierówności.Mógł ktoś zrobić literówkę i uczący nie zauważył. Masz rozwiązane dobrze. http://www.wolframalpha.com/input/?i=|x%2B1|%E2%89%A4+x%2F3%2B2+

Aga1.: Obydwa przykłady rozwiązałeś poprawnie, a co Ci nie daje spokoju?