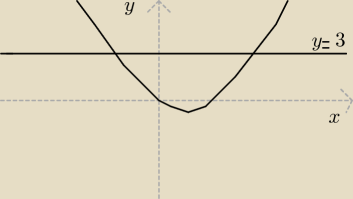
Proszę o pomoc z zad. z ograniczonymi krzywymi zuza: Wyznacz pole ograniczone krzywymi: y = x²−2x ⋀ y=3.

Jacek Karaśkiewicz: f(x) = x² − 2x Aby móc obliczyć pole ograniczone krzywymi y = x² − 2x i y = 3 dokonamy przekształcenia funkcji f. Po pierwsze odbijemy ją względem osi OX: f → −f. Musimy jeszcze "podnieść" wykres o 3: f → f + 3 Otrzymujemy nową funkcję g(x) = −x² + 2x + 3. Interesuje nas teraz całka Riemanna z tej funkcji na przedziale [x₀, x₁], gdzie x₀ < x₁, i g(x₀) = g(x₁) = 0. Pierwiastkami funkcji g są: x₀ = −1, x₁ = 3. ∫_{[−1, 3]} g(x)dx = ∫_{[−1, 3]} (−x² + 2x + 3) dx = [−^x3₃ + x² + 3x]₋₁³ = = (−9 + 9 + 9) − (¹₃ + 1 − 3) = 11 − ¹₃ = ³²₃

zuza: dziękuję

Damian: Prosto i szybko zrobione rzadko widuje tu zadania ze studiów... a szkoda

zuza: a ja mam masę zadań ze studiów... w dodatku czasami poprostu nie wiem jak do nich podejść... bo później to już leci