Okrąg wpisany w trójkąt prostokątny luck00: Promień okręgu wpisanego w trójkąt prostokątny jest równy r, a jeden z kątów ostrych ma miarę α. Wyznacz pole tego trójkąta. Nie wiem jak zrobić to zadanie. Będę wdzięczny za pomoc. Pozdrawiam

luck00: no i co? da rade coś wymyśleć

Krzysiek: pewnie ze da

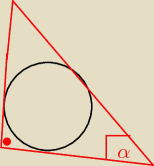
Krzysiek: skorzystaj z tw sinusow, z tozsamosci trygonometrycznych, no i ewentualnie z tw pitagorasa

imię lub nick:

	α		r		r
tg		=		⇒x=
	2		x		α   tg   2

	α   r(1+tg )   2
|AC|=r+x=
	α   tg   2

	|BC|		α   r*tgα(1+tg )   2
tgα=		⇒ |BC|=
	|AC|		α   tg   2

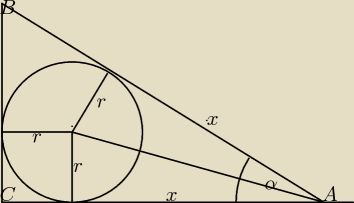
	r(1+tgα2)   r*tgα(1+tgα2)   * tgα2   tgα2
P=		=
	2

	r2tgα(1+tgα2)
	tgα2

imię lub nick: k∪ℛω∀... się kliknęło... w dupie to mam idę spać...

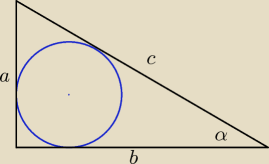
Bogdan: r − długość promienia okręgu wpisanego. Korzystamy z zależności: 2r = a + b − c oraz z: a = c sinα i b = c cosα

	2r
2r = c sinα + c cosα − c ⇒ c =
	sinα + cosα − 1

	2rsina		2rcosα
a =		, b =
	sinα + cosα − 1		sinα + cosα − 1

	1
pole trójkąta P =		ab, wystarczy podstawić tu wyznaczone a oraz b.
	2