analityczna matura_z_matematyki: Wyznacz równanie okręgu będącego obrazem okręgu (x−5)²+(y−2)²=9 w symetrii względem prostej l: y=2x−3. Obliczyłem prostą prostopadłą do prostej l i odległość środka okregu od tej prostej, wg mnie potrzebuję jeszcze środka drugiego okręgu ale nie wiem jak go obliczyć. Możecie mi pomóc

matura_z_matematyki: heeej heeej jest tam ktooooo

@Basia: Jeżeli masz prostą k prostopadłą do l i przechodzącą przez środek O₁ Twojego okręgu to: O₂ − środek drugiego okregu S − punkt przecięcia prostych k, l znajdź współrzędne S O₁S^→ = SO₂^→

Eta: Punkt przecięcia danej prostej i prostej prostopadłej jest środkiem odcinka S₁S₂ może to Ci coś wyjaśni

matura_z_matematyki: Wybaczcie mi ale ja dalej nie moge wpaść na to... Obliczyłem ten punkt i co dalej?

matura_z_matematyki: Chyba już wiem dajcie mi sek

@Basia: wektory równe mają równe współrzedne albo wzór na współrzędne środka odcinka

Eta: x_S2 = 2x_P − x_S1 y_S2 = 2y_P − x_S1

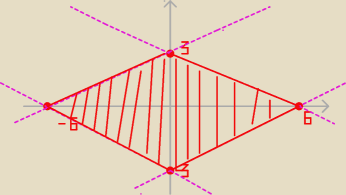
matura_z_matematyki: Już sobie poradziłem dzieki Mam tu kolejną "perełkę": Narysuj figurę określoną nierównością |1/2x|+|y|<=3 Zrobiłem to tak, że narysowałem wykres tej funkcji bez wartości bezwz. i tylko odbiłem od osi w odpowiednich miejscach ale coś czuje że to nie jest dobra metoda i trzeba to pewnie jakoś policzyć. Czekam na wasze sugestie

matura_z_matematyki: Cierpliwie czekam nigdzie nie idę

Eta:

matura_z_matematyki: Nie no ładnie pięknie wszytko tylko skad

matura_z_matematyki: no i oczywiście moja metoda była nie do końca trafna

Eta: Mówi Ci to coś? rozpatrujesz przedziałami: 1/ x≥ i y≥0 masz : ¹₂x + y ≤3 zatem prosta ma równanie: y = 3 − ¹₂x miejsce zerowe to x = 6 przechodzi zatem przez punkty ( 6,0 ) i ( 0,3) czyliwybirerasz zb. punktów pod ta prostą tylko dla x≥o i y≥) 2/ podbnie ale dla x<0 y≥0 czyli : −¹₂x + y ≤ 3 to prosta ma równanie: y = +¹₂x +3 miejsce zerowe x= −6 ( −6,0) i ( 0,3) zbiór punktów teź pod ta prosta i wraz z nią , dla x<0 i y≥0 itd.................................... poradzisz już sobie

matura_z_matematyki: CZyli to trzeba było przedziałami rozpatrywać... no coś w tym jest Dobra to zrobię to i bede miał jeszcze z jedno zadanko mam wene dzisiaj na matamatykę

Eta: Zobacz teraz skąd Napisz mi czy wiesz Czekam w pozostałych przypadkach pamietaj , tam będzie zmiana zwrotu nierówności

matura_z_matematyki: Tak Eta juz wszystko rozumiem, pamiętam o zmianie zwrotu pamietam, dziekuję za troskę

Eta: OK

matura_z_matematyki: Wpadnij za chwilę jak będę miał nast zadanie ok

Eta: Ok ....... narazie idę coś zjeść

matura_z_matematyki: Smacznego

matura_z_matematyki: no i wszystko ładnie pięknie wyszło tak jak podpowiedziałaś A oto i obiecane zadanie: Wyznacz punkt P jednakowo odległy od prostej l: y=−2 i punktu F = (0,2). Ile jest takich punktów i gdzie leżą

@Basia: P(x,y) równanie l: przekształcamy do postaci ogólnej 0*x + 1*y + 2 = 0 zapisz |FP| zapisz d(F,l) porównaj (podnieś obustronnie do kwadratu)

Eta: Jestem już P(x,y) F( 0,2) punkt leżacy na prostej y = −2 ma współrzedne : A( x, −2) porównujemy długości: IPFI=IPAI IPFI² = x² +(y −2)² IPAI² = 0 + ( y +2)² otrzymasz: x² + y² −4y +4 = y² +4y +4 => −8y = −x² to y = ^x2₈ −−−−−−− to parabola zbiór takich punktów znajduje sie na tej paraboli

Eta: Basia odbiera mi przyjemność pomagania

matura_z_matematyki: No Panie walczą, żeby mi pomóc Hehe cieszę się bardzo xD Wracając do zadania doszedłem do tego równania − x²= −8y i nie wiedziałem co dalej ale już wszystko rozumiem. Dobra lekki sen mnie bierze, więc nie ma sensu się męczyć. Jutro tu wróce Dziękuje serdecznie za pomoc Dobranoc

Eta: Miłego snu

Kasia: Parze na to pierwsze zadanie i miomo wytłumaczenia nie rozumiem, wyznaczyłam sobie promień, srodek okręgu i nie wiem czy dobrze wyznaczam proste : y= 1/2x −2 czyli prosta prostopadła to y=−2x+b ?

Kasia: jezeli dobrze proste to co z nimi mam zrobic dalej? help