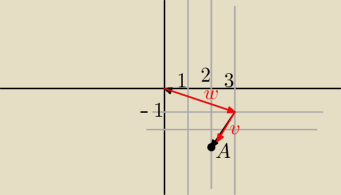
PROblem TOmek: Dany jest punkt A(2; 3) i wektor v[1; 2]. Czy punkt (10,−10); nalezy do prostej A + tv? −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Narysowałem sobie to jak na rysunku. w=[3,−1] v=[−1,2] czyli równanie parametryczne prostej x=3−t y=−1+2t 10=3−t => t=7

	9
−10=−1+2t => t=
	2

czyli nie nalezy.. dobrze?

TOmek:

TOmek: ?

TOmek: Dowieść ,ze dla kazdej liczby naturalnej n zachodzi nierownosc 10n<2ⁿ+25 −−−−−−−−−− sprawdzam dla n=1 10<26 niech n bedzie taka liczba naturalna ,ze 10n<2ⁿ+25 wowaczas udowodnie ,ze 10(n+1)<nⁿ⁺¹+25 L=10n+10=2ⁿ+25+10=2ⁿ+35 i nie wiem co dalej moze jakies przeskształcenie 2ⁿ+35≤2ⁿ⁺¹+35−2ⁿ Co w ten deseń ?

a: coś dużo osób z uniwerku ma problemy z indukcją [indukcja od n ≥ 4] 1,2,3 ręcznie

Krzysiek: zał: 10n<2ⁿ +25 teza: 10(n+1)<2ⁿ⁺¹ +25 10(n+1)=10n+10<2ⁿ +25+10 =2ⁿ+35 trzeba sprawdzić czy: 2ⁿ +35 ≤2ⁿ⁺¹ +25 10≤2ⁿ (2−1) =2ⁿ a to dla n≥4 zachodzi czyli 10(n+1) <2ⁿ⁺¹ +25

a: indukcja od n ≥ 4 rzecz jasna dla 2ⁿ + 35 < 2^{n + 1} + 25

TOmek: danke