. aaamm: co to jest zbiór wierzchołków parabol potrzebne do zadania a nie moge obczaic

konrad: zbiór zawierający wierzchołki parabol może podaj całą treść zadania

ICSP: zadanie z parametrem ?

Godzio: Zapewne chodzi o wyznaczenie takiej krzywej, która jest zbiorem wierzchołków parabol przy jakimś warunku ... Zbiór to zbiór Punkty na płaszczyźnie (bo chodzi nam tylko o wierzchołki), ponieważ jest ich duuużo to utworzą jakąś krzywą

aaamm: wyznacz zbiór punktów, utworzony z wirzchołków parabol o równaniach : y=2(x−3)²+m y=1/2(x+2)²−m Nie wiem o co tu "camman" : i w ogóle czy o to chodzi, że jest wiele parabol i one przecinają się w jakimś specyficznym punkcie i te punkty tworzą krzywą kurdeee nie wiem ...

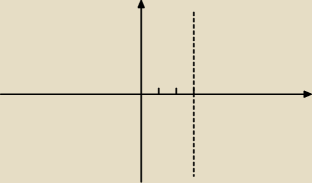
Godzio: y = 2(x − 3)² + m Zbiór tych wierzchołków to prosta x = 3 (bo pierwsza współrzędna jest stała, a druga jest dowolna) Pamiętamy, że współrzędne wierzchołka paraboli o równaniu: f(x) = a(x − p)² + q to : W(p,q)

aaamm: i w ogóle mama taki przykłąd w ksiażce ze wykres funkcji y=−(x−m)²+2 powstaje w wyniku przesunięcia równoległego o translacje [m,2] wykresu y=−x² i że wierzchołki parabol mają współrzędne (m,2) skąd to jest wiadomo, że mają takie współrzędne może to jest jeszcze akurat jakiś prostszy przykład, ale jak np jest funkcja y=−3x² i przesuniemy ją o translacje [m,2] to jak rozpoznać gdzie bedą teraz wierzchołki tych parabol ?

Godzio: Troszkę teoretycznie: y = f(x) − przesuwając tą funkcję o wektor [p,q] otrzymamy: y = f(x − p) + q, w wypadku funkcji kwadratowej postaci: otrzymamy postać kanoniczną, f(x) = a(x − p) + q −− z niej odczytujemy wierzchołek paraboli: W(p,q) i jednocześnie wektor przesunięcia funkcji: v = [p,q]

konrad: jak masz jakiś wektor [a,b] i masz jakaś funkcję którą masz o niego przesunąć, to od x odejmujesz a , a do y czyli do całej funkcji dodajesz b y=−3x² f. po przesunięciu o [m,2] y=−3(x−m)²+2

aaamm: czyli wierzchołek paraboli tej funkcji to też wektor przesunięcia. Tak jest we wszystkim przypadkach np. przesuwam funkcje o wekto [2,3] i punkt (2,3) jest wierzschołkiem paraboli. dobrze czaje ?

konrad: no jeżeli przesuwasz funkcję o wierzchołku (0,0) to tak

aaamm: a własnie, co sie dzieje skad mam wyczaic jak bedzie to funkcja nie o wierzchołku (0,0)?

Godzio: To najczęściej się liczy, podam przykład: f(x) = 2x² − 1 wierzchołek to (0,−1) przesuwamy o wektor: [2,3] i mamy: f(x) = 2(x − 2)² − 1 + 3 = 2(x − 2)² + 2 i teraz wierzchołek to (2,2)

Godzio: Są wzory na to, powinieneś je znać raczej

	−b		−Δ
f(x) = ax2 + bx + c i W(p,q) to p =		i q =
	2a		4a

aaamm: aha czyli jak mama niepewną sytuacje i jak nie wiem, czy wierzchołek znajduje się w jakims punkcie konkretnym, to podkałdam pod wzory ?

Godzio: Tak, do wzorów zawsze można podstawić

aaamm: dzieki wielkie !

konrad: ale nie zawsze trzeba

konrad: dobrze skumać postać kanoniczną, bo jak masz funkcję w takiej postaci to zaoszczędzisz trochę czasu na liczeniu współrzędnych wierzchołka