matematykaszkolna.pl
Liczby zespolone, przykład iwko: Jak obliczyć liczbę (1 − i√3 +i)6
6 paź 12:59
iwko: Rozjechało się, √3+1 są w mianowniku razem
6 paź 13:00
Aga1.: Tak ma wyglądać?
 1−i 
(
)6
 √3+1 
6 paź 13:01
iwko: Tak
6 paź 13:04
Aga1.: Najpierw zajmij się tym co jest w nawiasie
1−i (1−i)(√3−1) 
=
=
√3+1 (√3+1)(√3−1) 
dokończ
6 paź 13:07
sushi_gg6397228: pewnie w mainowniku jest √3 +i bo tak wyglada po zapisie w 1 linijce w 1 poscie
6 paź 13:09
iwko: to zrobiłem wcześniej, doszedłem do postaci. (√3−i−√3i−1)6/4
6 paź 13:12
iwko: tak w mianowniku miało być √3+i nie zuważyłem że to 1
6 paź 13:14
Aga1.:
 √3−1−i√3+i √3−1 1−√3 
Wychodzi
=
+
i
 2 2 2 
Teraz przedstaw tę liczbę w postaci trygonometrycznej i skorzystaj ze wzoru M...
6 paź 13:17
Aga1.: A to będzie inaczej
6 paź 13:17
Aga1.:
1−i (1−i)(√3−i) √3−i−√3i−1 
=
=
=
√3+i (√3+i)(√3−i) 4 
√3−1 −1−√3 
+
i
4 4 
6 paź 13:22
sushi_gg6397228: po co tak, liczysz osobno licznik, osobno mianownik −−> zamiana na postac trygonometryczna i de Moivre'a
6 paź 13:24
iwko: więc jak ostatecznie ma to wyglądać od początku do końca? W zadaniu nie chodziło o zapis w postaci trygonometrycznej, tylko o obliczenie
6 paź 13:33
sushi_gg6397228: jak piszesz w trygonometrii to potem sie moduły skroca, a katy zamieniesz na liczby
 a+bi 
a jak nie chcesz to dymasz do potegi 6 i bedzie
 c+di 
6 paź 13:37
iwko: Mógłbyś to zapisać we wzorze de Moivre'a jak powinno to wyglądać?
6 paź 13:57
sushi_gg6397228: najpierw zapisz obliczenia osobno do licznika, osobno do mianownika −−> zamiana na postac trygonometryczna
6 paź 13:58
iwko: Chyba nie rozumiem
6 paź 14:01
sushi_gg6397228: 1−i −−> zapisz w postaci trygonometrycznej
6 paź 14:02
iwko: √2(cosδ+isinδ)
6 paź 14:04
sushi_gg6397228: a ile wynosi kąt ?
6 paź 14:06
iwko: √2(cosπ/4+isinπ/4)
6 paź 14:10
iwko: a dla mianownika wyszło √2(cosπ/3+isinπ/3)
6 paź 14:16
sushi_gg6397228: to teraz podnosimy do potegi 6 Z6=|z|6 ( cos 6 * α + i sin 6*α ) uzywaj zapisu ułamkowego a nie a/b bo sie rozmywa
6 paź 14:30
sushi_gg6397228: 1−i to nie jest pierwsza ćwiartka tylko 4 wiec kat bedzie ...
6 paź 14:31
iwko: 54π
6 paź 14:33
iwko: aj błąd, 43π
6 paź 14:34
sushi_gg6397228: stosuj U to bedzie czytelniej dla ułamka 4 cwiartka ma 315 stopni =.... π
6 paź 14:37
iwko: ? Dlaczego 315?
6 paź 14:39
sushi_gg6397228: zaznacz ten punkt w ukladzie wspolrzednych (1,−1) lezy na prostej y=−x
6 paź 14:40
iwko: Już nie rozumiem zgubiłem się
6 paź 14:43
iwko: A już rozumiem skąd się to wzięło, błąd wcześniej popełmniłem
 7 
IV ćwiartka
π
 4 
6 paź 14:48
sushi_gg6397228: to zapisujemy jeszcze raz 1−i=.... postac trygonometryczna
6 paź 14:49
iwko:
 7 7 
1−i=√2(cos6*
π+isin6*
π)
 4 4 
6 paź 14:52
sushi_gg6397228:
 7 7 
z= 1−i= √2 ( cos
π + i sin
π)
 4 4 
z6= .... wzor co podalem o 14.30
6 paź 14:54
iwko:
 7 7 
Z6=√26(cos6*
π+isin6*
π)
 4 4 
6 paź 14:54
sushi_gg6397228: to teraz liczymy √26= ... to co jest w argumencie kąta skracamy i mamy ...
6 paź 14:57
iwko: √26=√2(cosπ+isinπ)?
6 paź 15:04
iwko: nie, nie wiem
6 paź 15:12
iwko: Może ktoś mi z tym pomóc?
6 paź 15:37
iwko: Po policzeniu licznika i podzieleniu przez mianownik, wyszło mi 1/8 czy to dobrze?
6 paź 17:19
Mila: Wynik:
−i 
8 
6 paź 18:15
iwko: Możesz pokazać swoje obliczenia?
6 paź 18:20
Mila: Tak, już piszę.
6 paź 18:51
Mila:
 1−i (1−i)*(√3−i) 
(
)6=(
)6=
 √3+i 3−i2 
 (1−i)6*(√3−i)6 
=
=...cd będzie
 46 
[ (1−i)6=[(1−i)2]3=(−2i)3=(−2)3*i3=8i ] [(√3−1)2]3=[(3−2√3i+i2]3=[2−2√3i]3=23*(1−√3)3= =8(1−3√3i+3*3i2−3√3i3)=8*(1−3√3i−9+3√3i)=8*(−8)=−64] łączę:
 8i*(−64) −8i −i 
cd...=
=
=
 43*43 64 8 
Mam nadzieję, że nie zrobiłam literówki przy przepisywaniu z kartki.
6 paź 19:05
Krzysiek: korzystając z postaci trygonometrycznej:
 1−i 
 7π 7π 
√2 (cos
+isin
)
 4 4 
 
(
)6 =(
)6 =
 √3+i 
 π π 
2(cos
+isin
)
 6 6 
 
 1 19π 19π 1 19π 19π 
=(
(cos
+isin
))6 =(
)6 *(cos
+isin
)
 √2 12 12 √2 2 2 
 1 
=
*(−i)
 8 
6 paź 19:16
iwko: Krzysiek nie rozumiem, od drugiej linjki Twojego rozwiązania. Tam jest jakieś dzielenie ?
6 paź 20:55
Krzysiek:
z1 |z1|(cosφ1 +isinφ1) 
=
=
z2  |z2|(cosφ2 +isinφ2 ) 
|z1| 
(cos(φ1 −φ2) +isin(φ1 −φ2) )
|z2| 
6 paź 21:03
Aga1.:
(√2)6 
=
26 
7 1 7 1 21−2 19 
π−
π=(
−
)π=
π=
π
4 6 4 6 12 12 
6 paź 21:05
iwko: Dziękuję bardzo wszystkim za pomoc!
6 paź 21:10
iwko: Zacząłem robić jeszcze kilka zadań i pojawiły się nowe problemy. znajdź i narysuj na płaszczyźnie zespolonej podane pierwiastki 6√−1−i oraz znaleźć pierwiastki równania kwadratowego −z√2+4=0 tu nie wychodzi mi liczba zespolona.
6 paź 21:32
Krzysiek: z=−1−i zamień na postać trygonometryczną http://pl.wikipedia.org/wiki/Wz%C3%B3r_de_Moivre'a co do drugiego zadania... popraw zapis, policz Δ
6 paź 21:37
iwko: −z2+4=0 tak miało być
6 paź 21:41
Krzysiek: wątpię żeby tak było... przecież: −z2 +4=0 z2 −4 =0 (z−2)(z+2)=0 czyli; z=2 lub z=−2 ...
6 paź 21:43
iwko: No właśnie, chyba poprostu coś źle przepisałem. a przykład −z2+z+1−i=0 po sprowadzeniu do równania kwadratowego bez liczby zespolonej wychodzi mi niewymierna delta Czy to jest dobrze?
6 paź 21:48
Krzysiek: Δ=5−4i √Δ =√5−4i =x+yi podnoszę stronami do kwadratu: 5−4i=(x+yi)2 i rozwiązujesz układ równań porównując części rzeczywiste i urojone
6 paź 21:53
iwko: Tak zrobiłem. po porównaniu wychodzi mi delta niewymierna.
6 paź 21:55
iwko: błąd rachunkowy, wszystko już ładnie wyszło
6 paź 21:59
Mila: Policz pierwiastki tego równania z takim wyrażeniem √5−4i
6 paź 22:03
iwko: w przykładzie 6√−1−i rozumiem że muszę liczyć 6 razy dla każdego n tak?
6 paź 22:17
Krzysiek: tak jak w linku dla każdego 'k' tzn, dla k=0,1,2,,3,4,5
6 paź 22:19
iwko: Mógłby mi ktoś policzyć dla k=0 w zadaniu ze wzorem De moivre'a? Bo mam z tym problemy.
7 paź 21:20
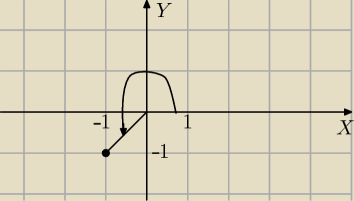
Mila: rysunekJeśli jest dużo komentarzy, to zakładaj nowy Post. z=−1−i |z|=√2 Aby wyznaczyć Φ korzystam z interpretacji geometrycznej liczby zespolonej.
 5π 
Φ=
 4 
 5π 5π 
z=|z|(cos
+isin
)
 4 4 
 
5π 
+2kπ
4 
 
5π 
+2kπ
4 
 
6√z=p12{2}*((cos
+isin
}
 6 6 
k=0
 
5π 
+0
4 
 
5π 
+0
4 
 
z1=p12{2}*(cos
+isin
}=
 6 6 
 5π 5π 
=p12{2}*(cos
+isin
)=...
 24 24 
k=1
 
5π 
+2π
4 
 
5π 
+2π
4 
 
z2=p12{2}*((cos
+isin
)=
 6 6 
 13π 13π 
=p12{2}*(cos
+isin
)=...
 24 24 
7 paź 22:16
iwko:
 5 
Do takiej postaci także dochodziłem, jednak nie wiedziałem jak pozbyć się
π
 24 
7 paź 22:26
iwko: Nie umiałem tego uprościc tak, aby wyszły jakieś konkretne wartości sin lub cos żeby można było to pomnożyc przez to co jest przed nawiasem.
7 paź 22:32
Mila: No nie zawsze wychodzą, zostawiasz w takiej postaci, albo odczytujesz przybliżone wartości. Zależy od potrzeby.
7 paź 22:36
iwko: Aha... straciłem mase czasu licząc ciągle dobrze i poprostu nie wiedząc że inaczej się uprościć nie da... Dziękuję bardzo za pomoc.
7 paź 22:38
iwko: A jak odczytać punkty, które muszę zaznaczyć na ukladzie wspolrzednych?
7 paź 22:39
Mila: Nie musisz zaznaczać, to taka moja metoda, bo ułatwia zlokalizować ćwiartkę dla Φ. 1+2i to punkt (1,2) 2−3i to punkt (2,−3) To, że liczyłeś długo, to nie strata czasu − zaprocentuje.
7 paź 23:01
iwko: no wiem że 1+2i to (1,2) ale skad to sie wzielo ? Bo w tym zadaniu ma być 6 punktów do zaznaczenia, a na wejściówce będę musiał zaznaczyć na układzie.
8 paź 14:07
Mila: Rysujesz okrąg o promieniu R=2{1/12) ( trochę ponad 1) i rysujesz po kolei kąty
 5π 
Przykład dla Φ=
=37,50.
 24 
http://www.wolframalpha.com/input/?i=2^%281%2F12%29*%28cos%285pi%2F24%29%2Bisin%285pi%2F24%29
8 paź 15:10
Mila: R=21/12
8 paź 15:23